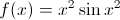Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivatives

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #294 : Computation Of The Derivative

Use the chain rule to differentiate the following function: $h(x)=sin(x^{2}e^{x})$

Possible Answers:

$h^{'}(x)=-sin(x^{2}e^{x})xe^{x}(2+x)$

$h^{'}(x)=cos(x^{2}e^{x})xe^{x}(2+x)$

$h^{'}(x)=-cos(x^{2}e^{x})xe^{x}(2+x)$

$h^{'}(x)=sin(x^{2}e^{x})xe^{x}(2+x)$

Correct answer:

$h^{'}(x)=cos(x^{2}e^{x})xe^{x}(2+x)$

Explanation:

$h(x)=sin(x^{2}e^{x})$

By the chain rule: $h^{'}(x)=cos(x^{2}e^{x})\frac{\mathrm{d} }{\mathrm{d} x}(x^{2}e^{x})$

Differentiate $(x^{2}e^{x})$ using the product rule: $\frac{\mathrm{d} }{\mathrm{d} x}(x^{2}e^{x})=\frac{\mathrm{d} }{\mathrm{d} x}(x^{2})e^{x}+x^{2}\frac{\mathrm{d} }{\mathrm{d} x}e^{x}=2xe^{x}+x^{2}e^{x}$

Substitute this derivative for $\frac{\mathrm{d} }{\mathrm{d} x}(x^{2}e^{x})$ in the first equation: $h^{'}(x)=cos(x^{2}e^{x})(2xe^{x}+x^{2}e^{x})$

Factor the equation: $h^{'}(x)=cos(x^{2}e^{x})xe^{x}(2+x)$

Report an Error

Example Question #295 : Computation Of The Derivative

f(p)=cos(2p-1)-(2p^3+4p)

Find f'(p) .

Possible Answers:

f'(p)=cos(2p-1)+sin(2p-1)-6p^2+4

f'(p)=-2cos(2p-1)(p^3+3p^2+2p+2)

f'(p) is undefined.

f'(p)=sin(2p-1)-sin(2p^3+4p)

f'(p)=-2(sin(2p-1)+3p^2+2)

Correct answer:

f'(p)=-2(sin(2p-1)+3p^2+2)

Explanation:

$\frac{d}{dx}[cos(2p-1)]=2 \cdot -sin(2p-1)=-2sin(2p-1)$

$\frac{d}{dx}[2p^3+4p]=6p^2+4$

Therefore:

f'(p)=-2sin(2p-1)-(6p^2+4)

=-2sin(2p-1)-6p^2-4

=-2(sin(2p-1)+3p^2+2)

f'(p)=-2(3p^2+sin(2p-1)+2)

Report an Error

Example Question #1 : Continunity As A Property Of Functions

Which of the following functions contains a removeable discontinuity?

Possible Answers:

$f(x)=\frac{x}{1-x^{2}}$

$f(x)=x^{2}\sin x^{2}$

$f(x)=\frac{x+1}{1+x^{2}}$

$f(x)=\frac{1+x^{3}}{1+x}$

$f(x)=1-(\ln x)^{2}$

Correct answer:

$f(x)=\frac{1+x^{3}}{1+x}$

Explanation:

A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at x=a , then the limit as approaches exists, but the value of f(a) does not.

For example, the function $f(x)=\frac{1+x^3}{1+x}$ contains a removeable discontinuity at x=-1 . Notice that we could simplify f(x) as follows:

$f(x)=\frac{1+x^3}{1+x}=\frac{(1+x)(x^2-x+1)}{1+x}=x^{2}-x+1$ , where $x\neq -1$ .

Thus, we could say that $\lim_{x\rightarrow -1}\frac{1+x^3}{1+x}=\lim_{x\rightarrow -1}x^2-x+1=(-1)^2-(-1)+1=3$ .

As we can see, the limit of f(x) exists at x=-1 , even though f(-1) is undefined.

What this means is that f(x) will look just like the parabola with the equation $x^{2}-x+1$ EXCEPT when x=-1 , where there will be a hole in the graph. However, if we were to just define f(-1)=3 , then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at x=-1 .

The functions

$f(x)=\frac{x}{1-x^{2}}$ , and

$f(x)=1-(\ln x)^{2}$

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.

The functions

$f(x)=x^{2}\sin x^{2}$ and $f(x)=\frac{x+1}{1+x^{2}}$ are continuous over all the real values of ; they have no discontinuities of any kind.

The answer is

$f(x)=\frac{1+x^{3}}{1+x}$ .

Report an Error

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&\text{Approximate a forward derivative at }x=4\\&\text{Using the following table:}\\&x&&f(x)\\&1&&5\\&4&&-8\\&7&&15\end{align*}$

Possible Answers:

$\frac{23}{6}$

$-\frac{13}{3}$

$\frac{23}{3}$

$-\frac{8}{3}$

Correct answer:

$\frac{23}{3}$

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(4)\text{ and }f(7)\\&\text{Applying the formula above, with }h=3\text{, we find:}\\&f'(4)\approx\frac{15-(15)}{3}\\&f'(4)\approx\frac{23}{3}\end{align*}$

Report an Error

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&x&f(x)\\&1&-27\\&3&-38\\&5&11\\&7&-5\\&9&-4\\&11&16\\&13&27\\&15&-15\\&\text{Using the above table, make a forward derivative approximation at }x=9\end{align*}$

Possible Answers:

$\frac{1}{2}$

Correct answer:

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(9)\text{ and }f(11)\\&\text{Applying the formula above, with }h=2\text{, we find:}\\&f'(9)\approx\frac{16-(16)}{2}\\&f'(9)\approx10\end{align*}$

Report an Error

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&\text{Approximate a forward derivative at }x=7\\&\text{Using the following table:}\\&x&f(x)\\&1&8\\&3&4\\&5&37\\&7&-24\\&9&-18\\&11&-38\\&13&44\end{align*}$

Possible Answers:

$-\frac{61}{2}$

$\frac{3}{2}$

Correct answer:

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(7)\text{ and }f(9)\\&\text{Applying the formula above, with }h=2\text{, we find:}\\&f'(7)\approx\frac{-18-(-18)}{2}\\&f'(7)\approx3\end{align*}$

Report an Error

Example Question #2 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&\text{Approximate a forward derivative at }x=0\\&\text{Using the following table:}\\&x&f(x)\\&0&22\\&4&2\\&8&50\\&12&-28\\&16&-40\\&20&-39\end{align*}$

Possible Answers:

$\frac{11}{2}$

$-\frac{5}{2}$

$\frac{11}{2}$

$-\frac{39}{2}$

Correct answer:

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(0)\text{ and }f(4)\\&\text{Applying the formula above, with }h=4\text{, we find:}\\&f'(0)\approx\frac{2-(2)}{4}\\&f'(0)\approx-5\end{align*}$

Report an Error

Example Question #4 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&\text{Approximate a forward derivative at }x=9\\&\text{Using the following table:}\\&x&f(x)\\&1&27\\&5&44\\&9&48\\&13&-31\\&17&-36\end{align*}$

Possible Answers:

$-\frac{79}{4}$

$-\frac{79}{8}$

Correct answer:

$-\frac{79}{4}$

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(9)\text{ and }f(13)\\&\text{Applying the formula above, with }h=4\text{, we find:}\\&f'(9)\approx\frac{-31-(-31)}{4}\\&f'(9)\approx-\frac{79}{4}\end{align*}$

Report an Error

Example Question #5 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&x&f(x)\\&0&-11\\&5&17\\&10&24\\&15&2\\&20&-15\\&25&-35\\&\text{Approximate a forward derivative at }x=10\end{align*}$

Possible Answers:

$\frac{24}{5}$

$-\frac{11}{5}$

$-\frac{22}{5}$

$\frac{7}{5}$

Correct answer:

$-\frac{22}{5}$

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(10)\text{ and }f(15)\\&\text{Applying the formula above, with }h=5\text{, we find:}\\&f'(10)\approx\frac{2-(2)}{5}\\&f'(10)\approx-\frac{22}{5}\end{align*}$

Report an Error

Example Question #6 : Approximate Rate Of Change From Graphs And Tables Of Values

$\begin{align*}&\text{Approximate a forward derivative at }x=0\\&\text{Using the following table:}\\&x&f(x)\\&0&19\\&2&-14\\&4&24\\&6&-11\\&8&19\\&10&21\\&12&-6\end{align*}$

Possible Answers:

$\frac{19}{2}$

$-\frac{33}{4}$

$-\frac{33}{2}$

Correct answer:

$-\frac{33}{2}$

Explanation:

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(0)\text{ and }f(2)\\&\text{Applying the formula above, with }h=2\text{, we find:}\\&f'(0)\approx\frac{-14-(-14)}{2}\\&f'(0)\approx-\frac{33}{2}\end{align*}$

Report an Error

View AP Calculus AB Tutors

Gary
Certified Tutor

SUNY at Albany, Bachelor of Science, Economics. Pace University-New York, Masters in Business Administration, Analysis and Fu...

View AP Calculus AB Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View AP Calculus AB Tutors

Emily
Certified Tutor

University of Michigan-Ann Arbor, Bachelor of Science, Public Health.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Houston, Calculus Tutors in Chicago, GMAT Tutors in Houston, ISEE Tutors in Los Angeles, LSAT Tutors in Los Angeles, Chemistry Tutors in San Francisco-Bay Area, SAT Tutors in Chicago, GRE Tutors in New York City, ISEE Tutors in Miami, ISEE Tutors in San Francisco-Bay Area

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in New York City, SSAT Courses & Classes in Seattle, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in Seattle, Spanish Courses & Classes in Seattle, SAT Courses & Classes in San Diego, LSAT Courses & Classes in Boston, ACT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Atlanta

Popular Test Prep

SAT Test Prep in Houston, GMAT Test Prep in New York City, MCAT Test Prep in Atlanta, ACT Test Prep in Philadelphia, LSAT Test Prep in Houston, MCAT Test Prep in Boston, GMAT Test Prep in Los Angeles, ISEE Test Prep in Boston, ACT Test Prep in Houston, GMAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivatives

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #294 : Computation Of The Derivative

Example Question #295 : Computation Of The Derivative

Example Question #1 : Continunity As A Property Of Functions

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #1 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #2 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #4 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #5 : Approximate Rate Of Change From Graphs And Tables Of Values

Example Question #6 : Approximate Rate Of Change From Graphs And Tables Of Values

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: