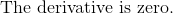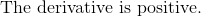Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivative at a point

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #22 : Slope Of A Curve At A Point

Find the slope of the line tangent to the function

$g(x)=x^2\cos(x)$

at $x=\pi$

Possible Answers:

$\pi$

$-2\pi$

$2\pi$

Correct answer:

$-2\pi$

Explanation:

The slope of the line tangent to a function is nothing more than the first derivative, which is for this function equal to

$g'(x)=2x\cos(x)-x^2\sin(x)$

found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Evaluated at the given point, we find the slope of the tangent line equal to

$g'(\pi)=2\pi(\cos(\pi))-\pi^2(\sin(\pi))=-2\pi$

Report an Error

Example Question #42 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine the sign of the derivative of the function above at the point }\\&x=2\end{align*}$

Possible Answers:

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=2\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #43 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine the sign of the derivative of the function above at the point }\\&x=4\end{align*}$

Possible Answers:

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is negative.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=4\text{, the function appears to be decreasing.}\\&\text{The derivative is negative.}\end{align*}$

Report an Error

Example Question #44 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine the sign of the derivative of the function above at the point }\\&x=3\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=3\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #142 : Ap Calculus Ab

Functionplot

$\begin{align*}&\text{Determine the sign of the derivative of the function above at the point }\\&x=-0.3\end{align*}$

Possible Answers:

$\text{The derivative is zero}$

$\text{The derivative is positive.}$

$\text{The derivative is negative.}$

Correct answer:

$\text{The derivative is zero}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-0.3\text{, the function appears to be flat.}\\&\text{The derivative is zero}\end{align*}$

Report an Error

Example Question #46 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine the sign of the derivative of the function above at the point }\\&x=0.2\end{align*}$

Possible Answers:

$\text{The derivative is negative.}$

$\text{The derivative is zero}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is zero}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=0.2\text{, the function appears to be flat.}\\&\text{The derivative is zero}\end{align*}$

Report an Error

Example Question #141 : Ap Calculus Ab

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=-1\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is negative.}$

$\text{The derivative is zero.}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is negative.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-1\text{, the function appears to be decreasing.}\\&\text{The derivative is negative.}\end{align*}$

Report an Error

Example Question #31 : Slope Of A Curve At A Point

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=-1\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-1\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #32 : Slope Of A Curve At A Point

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=7\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is zero.}$

$\text{The derivative is positive.}$

$\text{The derivative is negative.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=7\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #33 : Slope Of A Curve At A Point

Functionplot

$\begin{align*}&\text{Conclude if the derivative of the function above at the point }\\&x=3\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is negative.}$

$\text{The derivative is zero.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=3\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

View AP Calculus AB Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

View AP Calculus AB Tutors

Austin
Certified Tutor

University of Arizona, Bachelor of Science, Physiology.

View AP Calculus AB Tutors

Shakeel
Certified Tutor

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Washington DC, LSAT Tutors in Houston, Computer Science Tutors in Phoenix, LSAT Tutors in Los Angeles, SAT Tutors in Miami, ACT Tutors in San Diego, Math Tutors in Dallas Fort Worth, Chemistry Tutors in Los Angeles, Algebra Tutors in Dallas Fort Worth, ISEE Tutors in Houston

Popular Courses & Classes

ISEE Courses & Classes in Washington DC, ISEE Courses & Classes in Seattle, ACT Courses & Classes in New York City, SAT Courses & Classes in Chicago, GRE Courses & Classes in Miami, SSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Houston, ACT Courses & Classes in San Diego, SAT Courses & Classes in Houston, Spanish Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in Phoenix, GMAT Test Prep in Miami, ISEE Test Prep in Houston, MCAT Test Prep in Washington DC, MCAT Test Prep in Los Angeles, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, SAT Test Prep in Houston, LSAT Test Prep in Philadelphia, ACT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivative at a point

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #22 : Slope Of A Curve At A Point

Example Question #42 : Derivative At A Point

Example Question #43 : Derivative At A Point

Example Question #44 : Derivative At A Point

Example Question #142 : Ap Calculus Ab

Example Question #46 : Derivative At A Point

Example Question #141 : Ap Calculus Ab

Example Question #31 : Slope Of A Curve At A Point

Example Question #32 : Slope Of A Curve At A Point

Example Question #33 : Slope Of A Curve At A Point

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: