All AP Calculus AB Resources
Example Questions
Example Question #231 : Derivatives
Find of the following equation:
To find we must use implicit differentiation, which is an application of the chain rule.
Taking of both sides of the equation, we get
using the following rules:
, ,
Note that for every derivative of a function with y, the additional term appears; this is because of the chain rule, where , so to speak, for the function it appears in.
Using algebra to rearrange, we get
Example Question #232 : Derivatives
Find the derivative:
The derivative of the function is equal to
and was found using the following rules:
, , ,
Before simplification, the derivative we get is
Note that the square root, the exponential, and the tangent function all utilize chain rule when taking their derivatives.
Example Question #233 : Derivatives
Find the first derivative of the following function:
The derivative of the function is equal to
and was found using the following rules:
, , ,
Note that the first rule - the chain rule - was used three times for the function: the cosine, contained the exponential which itself was raised to a function. (Note that sometimes the exponential rule is written as , which itself is the chain rule.)
Example Question #234 : Derivatives
A reaction is modeled by the following equation:
where are constants.
What is ?
The derivative of the function is equal to
and was found using the following rules:
, ,
The chain rule was used for the function contained in the exponential function (or, as written as a rule, ).
Example Question #235 : Derivatives
For the equation, , find .
The equation given is not written and . Instead, it is written with 's and 's on the same side of the equation. This suggests we should try implicit differentiation, which means find the derivative of both sides with respect to .
"With respect to " means that we treat every other variable as a function of . So , and the derivative of is a chain rule. This will be emphasized later in the explanation.
First we must differentiate both sides with respect to .
We have multiple terms on the left hand side, so we will differentiate each term individually.
For the first term, , we will use the power rule and also use the chain rule, since we must assume that .
The blue part is the power rule. The red is from the chain rule. The red part is the derivative of y with respect to x, which is currently unknown. Remember that y is some unknown function of x, whose derivative is also unknown. We can only write for the derivative of y.
Now we find the second term's derivative,
This is a product rule. To help with the product rule, the two pieces are color coded. Remember that the power rule is
Applying this, we get
Simplifying gives us
For the third term, , we will algebraically rewrite it as , so we can apply the product rule instead of the quotient rule. This is just a personal preference, The quotient rule would work as well.
remember that the derivative of with respect to requires the chain rule, resulting in the .Simplifying gives us
The right hand side of the equation is a constant, so its derivative is zero.
Assembling all the parts back together, we have
Now that we have differentiated the equation, we need to algebraically solve for .
First, we should move all terms with a to one side, which in this case is already done. Then we should move all terms without a to the opposite side of the equation. Doing so, we get
Then we will will factor out the common factor of . This results in
Then, to isolate , we divide both sides by .
Now we need to simplify and get rid of the negative exponents. To do this, we can simply multiply the numerator and denominator by . This will result in
Which is the correct answer.
Example Question #236 : Derivatives
Given the function , find its derivative.
Given the function , we can find its derivative using the chain rule, which states that
where and for . We have and , which gives us
Example Question #237 : Derivatives
Given the function , find its derivative.
Given the function , we can find its derivative using the chain rule, which states that
where and for . We have and , which gives us
Example Question #238 : Derivatives
Given the function , find its derivative.
Given the function , we can find its derivative using the chain rule, which states that
where and for . We have and , which gives us
Example Question #239 : Derivatives
Given the function , find its derivative.
Given the function , we can find its derivative using the chain rule, which states that
where and for . We have and , which gives us
Example Question #240 : Derivatives
Given the function , find its derivative.
Given the function , we can find its derivative using the chain rule, which states that
where and for . We have and , which gives us
Certified Tutor
Certified Tutor
All AP Calculus AB Resources



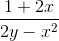


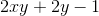





























































![\frac{\mathrm{d} }{\mathrm{d} x}[y^2 + 2x^2y - \frac{5x}{y}] = \frac{\mathrm{d} }{\mathrm{d} x}[2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967670/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[y^2] + \frac{\mathrm{d} }{\mathrm{d} x}[2x^2y] + \frac{\mathrm{d} }{\mathrm{d} x}[\frac{-5x}{y}] = \frac{\mathrm{d} }{\mathrm{d} x}[2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969699/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[y^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967672/gif.latex)

![\frac{\mathrm{d} }{\mathrm{d} x}[y^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967674/gif.latex)
![{\color{Blue} 2[y]^{2-1}}{\color{DarkRed} (\frac{\mathrm{d} y}{\mathrm{d} x})}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967675/gif.latex)


![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} 2x^2}{\color{DarkRed} y}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967678/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} f(x)}\cdot{\color{DarkRed} g(x)}] ={\color{Blue} f(x)}\cdot {\color{DarkRed} g'(x)} + {\color{Blue} f'(x)} \cdot {\color{DarkRed} g(x)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967679/gif.latex)




![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} -5x}{\color{DarkRed} y^{-1}}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969702/gif.latex)











![\frac{\mathrm{d} y}{\mathrm{d} x}[2y + 2x^2 + 5xy^{-2}] = -4xy + 5y^{-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969711/gif.latex)

![[2y + 2x^2 + 5xy^{-2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969713/gif.latex)





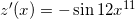




![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970854/gif.latex)












![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971039/gif.latex)












![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971030/gif.latex)












![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971052/gif.latex)












![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970993/gif.latex)









