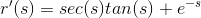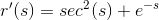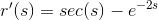All AP Calculus AB Resources
Example Questions
Example Question #91 : Chain Rule And Implicit Differentiation
Find
We will be using the following rule and the chain rule:
Also remember that
Now, looking at our function we are to find the derivative of,
We must use our first rule and the chain rule,
Let's rewrite that a little using our second rule,
Now let's use our first rule again (no further chain rule is required)
And now we just need to simplify,
So
Example Question #185 : Computation Of The Derivative
Find
We are going to use the following rules and the chain rule:
Now, looking at our original function,
can be written as
Then
Now we finish up by using the second rule backwards and then the first rule on the remainder (no more chain rule is required),
And finally, we have the derivative
Example Question #181 : Computation Of The Derivative
Compute the derivative of the following function:
Compute the derivative of the following function:
To find this derivative, we are going to use the chain rule:
What this means, is that we will take the derivative of the "outside" *in this case the 
So, let's jump in.
We can easily do our f' part. Doing so yields
Next, calculate the derivative of the inside.
Put that back together with the above part to get:
Clean it up a bit to get.
Which we will leave as...
Example Question #271 : Derivatives
Find the derivative of the function:
*****************************************************************
REQUIRED KNOWLEDGE
*****************************************************************
This problem requires us to understand two things:
1) The derivative of the function 

2) By adding an operation to the variable in the exponent (in our case, the -s instead of just s), we must multiply the derivative by the derivative of the argument in the exponent. This is an application of the chain rule of derivation
*****************************************************************
SOLUTION STEPS
*****************************************************************
Thus:

Thus, the correct answer is:
*****************************************************************
CORRECT ANSWER
*****************************************************************
*****************************************************************
PROBLEMS?
*****************************************************************
If you did not understand the concepts required to solve this derivative problem:
- Look into the derivative of e raised to an argument
- Practice applying the chain rule to derivative problems
Example Question #95 : Chain Rule And Implicit Differentiation
Find the derivative of the function:
*****************************************************************
STEPS
*****************************************************************
Given:
Let:
Now:
Now, we plug in sin^2(x) again
To find "chain", we must take the derivative of sin^2(x), using the product rule:
Plug in this new-found term into the chain in the above derivative:
Canceling the sin on top with a sin on bottom, we arrive at the correct answer:
*****************************************************************
CORRECT ANSWER
*****************************************************************
Example Question #96 : Chain Rule And Implicit Differentiation
Given:

Find:
*****************************************************************
STEPS
*****************************************************************
Understand that if:

then:
Rearrange this as such:
We are also given:
Thus,
Plugging in 3dt into our previous dx allows us to look for dy/dt
Rearranging, we arrive at the correct answer:
*****************************************************************
CORRECT ANSWER
*****************************************************************
Example Question #191 : Computation Of The Derivative
Find the derivative of the function:
*****************************************************************
STEPS
*****************************************************************
Given:
Implement the sin^-1 derivative:
Understand that we find our chained term by deriving the compound element(in this case, x^3)
Plug our new-found element in for the chain, and multiply accordingly:
After multiplying, we arrive at the correct answer:
*****************************************************************
ANSWER
*****************************************************************
Example Question #192 : Computation Of The Derivative
Find the derivative of the function:
*****************************************************************
STEPS
*****************************************************************
Given:
Apply the derivative of arc-tangent (tan^-1)
Understand that to find the (chain term), we must derive the compound function element, in this case it is (1-r^2)
Now, we plug -2r in for the chain term
Multiplying it across, we arrive at the final, correct answer:
*****************************************************************
ANSWER
*****************************************************************
Example Question #193 : Computation Of The Derivative
Find 


The derivative of the function is equal to
and was found using the following rules:



Note that because 
Example Question #191 : Computation Of The Derivative
Calculate the derivative of 
We know how to take the derivative of 

According to the chain rule, we should take the derivative of the outside function and multiply it by the derivative of the inside function. This gives us:
Remember that 
Our final answer:
All AP Calculus AB Resources