All AP Calculus AB Resources
Example Questions
Example Question #1 : How To Find Maximum Values
What is the local maximum of 


There is no maximum between these two points.
To find the maximum, we must find where the graph shifts from increasing to decreasing. To find out the rate at which the graph shifts from increasing to decreasing, we look at the second derivative and see when the value changes from positive to negative.
That is to say, we will look at the second derivative and see where (if at all) the graph crosses the x-axis and is moving from a positive y-value to a negative y-value.
Now we must find the second derivative. Unfortunately, the derivatives of trig functions must be memorized. The first derivative is:

To find the second derivative, we take the derivative of our result.

Therefore, the second derivative will be 
Does our new equation cross the x-axis and move from positive to negative between 




Example Question #1 : How To Find Maximum Values
Find the x coordinate of the maximum of 
![\left [ -1,2\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106365/gif.latex)
5
-2
0
6
2
2
First find the derivative, which is:
Set that equal to zero to get your critical points:
You also have to take into account -1 and 2 as critical points since those are your endpoints. Evaluate each of these critical points in the original function:
The greatest is your maximum. The x coordinate is 2.
Example Question #2 : How To Find Maximum Values
Find the value at which the function 
To find the maximum, we need to find the critical points. To do that, we need to take the derivatie of the function.
And we can see that 

An easy way to see which is the maximum and which is the minimum is to plug in the values of the critical points into the original equation.

Therefore, the maximum value is 3, and the value at which the function reaches the maximum is 0.
Example Question #3 : Techniques Of Antidifferentiation
Consider the function
Find the minimum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90588/gif.latex)
To find potential minima of the function, take the first derivative of 
Set the derivative to 0:
We solve for 

We can double check that 
which means the function is concave up, so that the point we found is a minimum.
Example Question #4 : Techniques Of Antidifferentiation
Find the x coordinate of the minimum of 
![\left [ -2, 2\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106125/gif.latex)
First, find the derivative, which is:
Set that equal to 0 to find your critical points:
Evaluate f at each critical point and endpoint over [-2, 2]:
The least of those numbers is the minimum. Because f(-2)=-32, that is the minimum.
Example Question #1 : Calculus I — Derivatives
What is the local minimum of 

There is no local minimum in that range.
The y-value is constant throughout that range.
To find the maximum, we need to look at the first derivative.
To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.
We're going to treat 

Notice that 
When looking at the first derivative, remember that if the output of this equation is positive, the original function is increasing. If the derivative is negative, then the function is decreasing.
Because we want the MINIMUM, we want to see where the derivative changes from negative to positive.
Notice that 


Example Question #1 : Techniques Of Antidifferentiation
Integrate,


Integrate
1) Apply the sum rule for integration,
2) Integrate each individual term and include a constant of integration,
Further Discussion
Since indefinite integration is essentially a reverse process of differentiation, check your result by computing its' derivative.
This is the same function we integrated, which confirms our result. Also, because the derivative of a constant is always zero, we must include "C" in our result since any constant added to any function will produce the same derivative.
Example Question #5 : Techniques Of Antidifferentiation
Example Question #1 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Example Question #2 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Certified Tutor
All AP Calculus AB Resources





















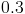
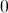
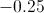





















![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749356/gif.latex)




![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749357/gif.latex)








![\begin{align*}&\text{In performing an integral, familiarity with derivative rules}\\&\text{can prove useful. After all, an integral is essentially the}\\&\text{opposite operation of a derivative. Consider how in a derivative}\\&\text{we’d use the chain rule to multiply the derivative of the “inside”}\\&\text{of a function by the derivative of the outside? Integrals, in}\\&\text{similar fashion, entail a division.}\\&\text{Utilizing integral rules:}\\&\int[cos(ax)]=\frac{sin(ax)}{a}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin(x + 1))}{8}|_{8}^{11.5}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin((11.5) + 1))}{8}-(\frac{(27sin((8) + 1))}{8})\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=-1.61\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931547/gif.latex)











![\begin{align*}&\text{In performing an integral, familiarity with derivative rules}\\&\text{can prove useful. After all, an integral is essentially the}\\&\text{opposite operation of a derivative. Consider how in a derivative}\\&\text{we’d use the chain rule to multiply the derivative of the “inside”}\\&\text{of a function by the derivative of the outside? Integrals, in}\\&\text{similar fashion, entail a division.}\\&\text{Utilizing integral rules:}\\&\int[b^{ax}]=\frac{b^{ax}}{aln(b)}\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=\frac{(40\cdot 2^{(\frac{x}{4})})}{(7ln(2))}|_{-6}^{-3}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=\frac{(40\cdot 2^{(\frac{(-3)}{4})})}{(7ln(2))}-(\frac{(40\cdot 2^{(\frac{(-6)}{4})})}{(7ln(2))})\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=1.99\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931641/gif.latex)



