All Algebra II Resources
Example Questions
Example Question #1 : Transformations Of Parabolic Functions
Consider the following two functions:

How is the function 













The 


Example Question #1 : Transformations Of Parabolic Functions
If the function 

Example Question #2 : Transformations Of Parabolic Functions
Select the function that accuratley fits the graph shown.
The parent function of a parabola is 

The original graph of a parabolic (quadratic) function has a vertex at (0,0) and shifts left or right by h units and up or down by k units.
.
This function then shifts 1 unit left, and 4 units down, and the negative in front of the squared term denotes a rotation over the x-axis.
Correct Answer:
Example Question #1 : Transformations Of Parabolic Functions
State the vertex of the following parabola
Without doing much work or manipulation of the function, we can use our knowledge of Vertex Form of quadratic functions, which is
with 




Note: This function is simply a transformation of the function
Example Question #5 : Transformations Of Parabolic Functions
Transform the following parabola: 
Shift up 

When transforming paraboloas, to translate up, add to the equation (or add to the Y).
To translate to the left, add to the X.
Don't forget that if you add to the X, then since X is squared, the addition to X must also be squared.


Now adding the shift to the left we get:

Example Question #3 : Transformations Of Parabolic Functions
Transform the following parabola 
Move 
Move 
To move unit down, subtract from Y (or from the entire equation) , so subtract 1.
To move unit to the left, add to X (don't forget, that since you are squaring X, you must square the addition as well).
With the move down our equation 

Now to move it to the left we get 
Example Question #1 : Transformations Of Parabolic Functions
Which function represents 


The parent function for a parabolic function is 

Example Question #1 : Transformations Of Parabolic Functions
Transformations of Parabolic Functions
Given the function:
write the equation of a new function 
Translations that effect x must be directly connected to x in the function and must also change the sign. So when the function was translated right two spaces, a 
Translation that effect y must be directly connected to the constant in the funtion - so when the function was translated up 4 spaces a +4 must be added to the (-5) in the original function.
When both of these happen in the function the new function
Example Question #1 : Transformations Of Parabolic Functions
List the transformations of the following function:
Compressed by a factor of 3
Horizontal translation to the left 2 units
Vertical translation down 5 units
Compressed by a factor of 3
Horizontal translation to the right 2 units
Vertical translation up 5 units
Compressed by a factor of 3
Horizontal translation to the left 2 units
Vertical translation up 5 units
Stretched by a factor of 3
Horizontal translation to the left 2 units
Vertical translation up 5 units
Stretched by a factor of 3
Horizontal translation to the right 5 units
Vertical translation up 2 units
Compressed by a factor of 3
Horizontal translation to the left 2 units
Vertical translation up 5 units
Because the parent function is 

a is the compression or stretch factor.
If 
If 
b represents how the function shifts horizontally.
If b is negative, the function shifts to the left b units.
If b is positive, the function shifts to the right b units.
c represents how the function shifts vertically.
If c is positive, the function shifts up c units.
If c is negative, the function shifts down c units.
For our problem, a=3, b=-2, and c=5. (Remember that even though b is negative, the negative from the "general form" makes the sign positive). It follows that we have a compression by a factor of 3, a horizontal shift to the left 2 units, and a vertical shift up 5 units.
Example Question #10 : Transformations Of Parabolic Functions
Translate the parabola 
To shift up 6 units, just add 6:

To shift to the right 3, subtract 3 from x:
First expand 
now this gives us:


All Algebra II Resources


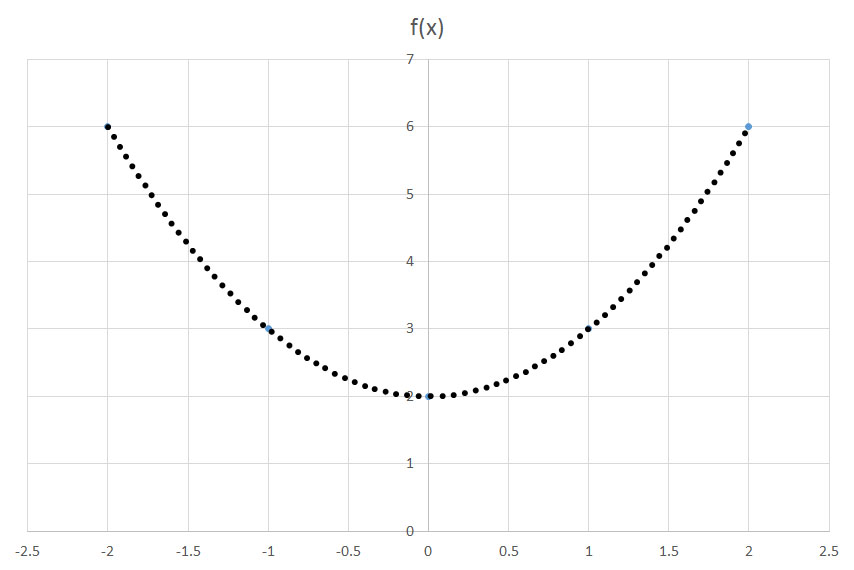



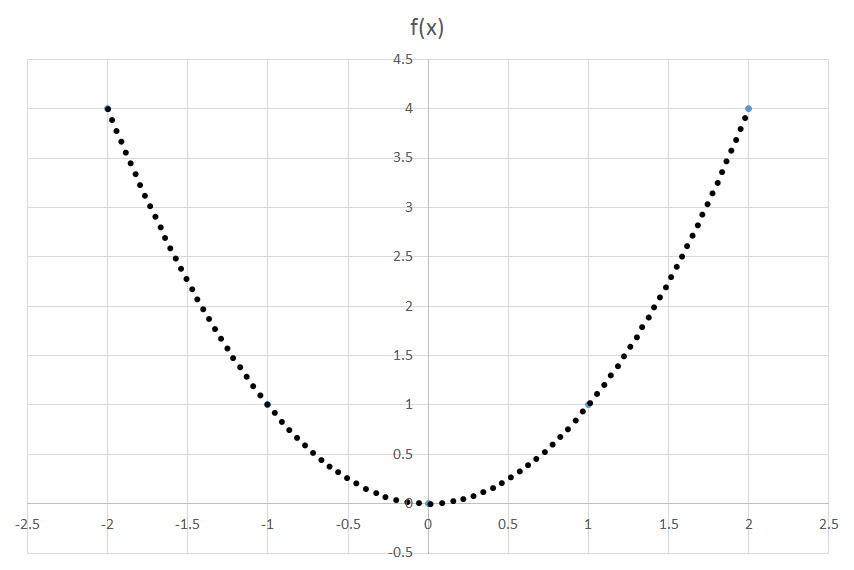
 shifts a function f(x)
shifts a function f(x)  units to the left. Conversely,
units to the left. Conversely,  shifts a function f(x)
shifts a function f(x)  units to the right. In this question, we are translating the graph two units to the left.
units to the right. In this question, we are translating the graph two units to the left. or
or  .
.
















































