All Algebra II Resources
Example Questions
Example Question #111 : Understanding Exponents
Simplify:
Simplify each term. The negative exponents can be rewritten as a fraction.
Add the fractions.
The answer is:
Example Question #112 : Exponents
Solve:
Convert each negative exponent to a fraction. Use the rule below to rewrite the terms.
The expression becomes:
Convert the denominators to a common LCD.
Reduce this fraction.
The answer is:
Example Question #113 : Exponents
Simplify the exponents:
The negative exponent can be rewritten as a fraction.
Divide this fraction with one-ninth.
Reduce the fraction.
The answer is:
Example Question #111 : Exponents
Solve:
The negative exponents must be rewritten in fractional form by the following rule.
This expression becomes:
Rewrite this complex fraction using a division sign. Take the reciprocal of the second term, and change the division sign to multiplication.
The answer is:
Example Question #115 : Exponents
Solve:
Evaluate both terms on the numerator and denominator separately.
We can rewrite the negative exponents as the reciprocal of the positive exponent.
Use the multiplicative rule of division to simplify the complex fraction.
Divide the two fractions.
The answer is:
Example Question #116 : Exponents
Simplify:
The negative exponents can be rewritten as fractions based on the following rule:
Rewrite all the terms in the parentheses.
Simplify the expression.
The answer is:
Example Question #117 : Exponents
Simplify:
The negative exponent can be rewritten as follows:
Rewrite the expression.
The answer is:
Example Question #581 : Mathematical Relationships And Basic Graphs
Simplify the following expression:
Example Question #1 : Exponents
Simplify the expression:
Remember that fraction exponents are the same as radicals.
A shortcut would be to express the terms as exponents and look for opportunities to cancel.
Either method, we then need to multiply to two terms.
Example Question #1 : Fractional Exponents
Convert the exponent to radical notation.
Remember that exponents in the denominator refer to the root of the term, while exponents in the numerator can be treated normally.
Certified Tutor
Certified Tutor
All Algebra II Resources





















































![[(2^{-3})\cdot (5^{-2})]^{-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/863627/gif.latex)






![[(2^{-3})\cdot (5^{-2})]^{-1} =[(\frac{1}{2^3})\cdot (\frac{1}{5^{2}})]^{-1} =[(\frac{1}{8})\cdot (\frac{1}{25})]^{-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/863632/gif.latex)
![[\frac{1}{200}]^{-1} = 1\div \frac{1}{200} = 1\times \frac{200}{1} = 200](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/863634/gif.latex)




















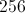


![256^{\frac{3}{4}}=\sqrt[4]{256^3}=64](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/113588/gif.latex)





![\small \small \sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39746/gif.latex)
![\small \small \sqrt[3]{x^7}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39747/gif.latex)

![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88792/gif.latex)
![x^{\frac{3}{7}}=\sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110623/gif.latex)



