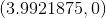All Algebra II Resources
Example Questions
Example Question #105 : Solving Exponential Equations
Solve:
Change the base of the fraction to base 2.
Now that both bases are similar, we can set the powers equal to each other.
Use distribution to simplify the right side.
Add 9 on both sides.
Divide by negative nine on both sides.
Reduce this fraction.
The answer is:
Example Question #106 : Solving Exponential Equations
Evaluate:
Change the base of the second number to base two.
We can then replace the term and use the power rule of exponents to simplify the equation.
Set the powers equal now that we have same bases.
Subtract 6 from both sides.
Divide by eight on both sides.
Reduce the fractions.
The answer is:
Example Question #101 : Solving Exponential Equations
Evaluate:
Convert the bases to 
Rewrite the terms of the equation.
With similar bases, we can set the powers equal to each other.
Simplify the right side by distribution.
Subtract six on both sides, and divide by negative six.
The answer is:
Example Question #108 : Solving Exponential Equations
Solve:
We can rewrite the fractional exponent as a radical.
Raise both sides by the power of four to eliminate the radical.
Add three on both sides.
Divide by two on both sides.
Reduce both fractions.
The answer is:
Example Question #109 : Solving Exponential Equations
Solve:
To be able to solve this equation, we will need to change the bases on both sides to a common base.
Choose three as the common base.
Replace the terms into the equation.
With the common bases, we can set the powers equal to each other.
Distribute the four on the right side.
Subtract 20 on both sides.
Divide by negative 12 on both sides.
Reduce both fractions.
The answer is:
Example Question #110 : Solving Exponential Equations
Solve:
Convert the bases to a common base so that the exponential powers can be set equal to each other. We can choose base two and rewrite both sides using exponential powers.
The radical is to the power of one-half.
Set the powers equal to each other.
Distribute the outer terms into the binomials.
Multiply by two on both sides to eliminate the fraction.
Add 
Subtract 40 on both sides.
Divide by 6 on both sides.
The answer is:
Example Question #1 : Graphing Exponential Functions
Give the 

The graph has no 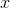
The graph has no 
Set 
We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of 

Example Question #21 : Solving Exponential Functions
What is/are the asymptote(s) of the graph of the function 

An exponential function of the form
has as its one and only asymptote the horizontal line 
Since we define 

then 
and the only asymptote is the line of the equation 
Example Question #1 : Graphing Exponential Functions
Determine whether each function represents exponential decay or growth.
a) growth
b) decay
a) decay
b) growth
a) growth
b) growth
a) decay
b) decay
a) decay
b) growth
a)
This is exponential decay since the base, 


b)
This is exponential growth since the base, 

Example Question #4 : Graphing Exponential Functions
Match each function with its graph.
1.
2.
3.
a.
b.
c.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
For 





For 



For 



Certified Tutor
All Algebra II Resources


















































![\sqrt[4]{2x-3}=3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/863928/gif.latex)
![(\sqrt[4]{2x-3} )^4=3^4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/863929/gif.latex)