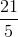Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Irrational Numbers

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5123 : Algebra Ii

Which of the below is NOT an irrational number?

Possible Answers:

$10-\pi$

$\sqrt{16}-\sqrt{49}$

$\sqrt{12}-3$

$\sqrt{-5}$

Correct answer:

$\sqrt{16}-\sqrt{49}$

Explanation:

The correct choice involves two perfect squares which makes each number a rational number:

$\sqrt{16}-\sqrt{49}=4-7=-3\ which\ is\ a\ rational\ number$

Report an Error

Example Question #32 : Irrational Numbers

Which of the following is an irrational number?

Possible Answers:

3.14159

$\sqrt{-3}$

$\sqrt{11}$

$1.6\%$

Correct answer:

$\sqrt{11}$

Explanation:

An irrational number is a number that cannot be rewritten as a ratio of two numbers such as $\pi$ or since their decimal numbers are continuous.

Square roots that are not perfect squares are irrational such as:

$\sqrt2, \sqrt5, \sqrt{11}$

Be careful with numbers that are fixed. Fixed numbers are finite and can be rewritten as a fractional term.

Imaginary numbers are neither irrational or real numbers and is defined as the term . The value of $\sqrt{-3}= i\sqrt3$ is an imaginary number. These are called complex numbers.

Percentages can be rewritten as a fraction.

The answer is: $\sqrt{11}$

Report an Error

Example Question #5124 : Algebra Ii

Try without a calculator.

True or false: the set

$\left \{ \sqrt {15}, \sqrt {16} , \sqrt {17}, \sqrt {18},\sqrt {19} \right \}$

comprises only irrational numbers.

Possible Answers:

False

True

Correct answer:

False

Explanation:

The square root of an integer is rational if and only if the integer is a perfect square of another integer.

$16 = 4 \times 4 = 4 ^{2}$ ,

so 16 is a perfect square, and $\sqrt{16}$ is a rational number. The statement is therefore false.

Report an Error

Example Question #5125 : Algebra Ii

Try without a calculator.

True or false: the set

$\left \{ 7 \pi , 8 \pi, 9 \pi, 10 \pi, 11 \pi \right \}$

comprises only irrational numbers.

Possible Answers:

False

True

Correct answer:

True

Explanation:

$\pi$ is an irrational number, as is any integer multiple of $\pi$ . All of the elements are integer multiples of $\pi$ , so all of them are irrational.

Report an Error

Example Question #5126 : Algebra Ii

Try without a calculator.

True or false: the set

$\left \{ 5e, 6e, 7e, 8e, 9e \right \}$

comprises only irrational numbers.

Possible Answers:

True

False

Correct answer:

True

Explanation:

is an irrational number, as is any integer multiple of . All of the elements are integer multiples of , so all of them are irrational.

Report an Error

Example Question #5127 : Algebra Ii

Which of the following represents an irrational number?

Possible Answers:

None of the numbers is irrational.

$-\sqrt{144}$

$0.\overline{3}$

$\sqrt{26}$

$-\frac{1}{1000}$

Correct answer:

$\sqrt{26}$

Explanation:

First, recall the definition of irrational numbers. Irrational numbers cannot be expressed as a ratio of integers.

The answer $0.\overline{3}$ is incorrect because it is a repeating decimal that can be rewritten as the following fraction:

$\frac{1}{3}$

In a similar vein, the following choice is already written as a simple fraction (negative numbers are not irrational):

$-\frac{1}{1000}$

It is important to note that not all square roots are irrational. For instance, the following square root can be simplified quite easily:

$-\sqrt{144} = -12$

The only answer that cannot be expressed as a simple fraction is:

$\sqrt{26}=5.09901951359278449161$

The answer is:

$\sqrt{26}$

Report an Error

Example Question #1 : Irrational Numbers

Which of the following is an irrational number?

Possible Answers:

5.75

$\pi$

$\sqrt{9}$

$0.\overline{3333}$

$\frac{21}{5}$

Correct answer:

$\pi$

Explanation:

A rational number can be expressed as a fraction of integers, while an irrational number cannot.

$0.\overline{3333}$ can be written as $\frac{1}{3}$ .

$\sqrt{9}$ is simply , which is a rational number.

The number 5.75 can be rewritten as a fraction of whole numbers, $\frac{23}{4}$ , which makes it a rational number.

$\frac{21}{5}$ is also a rational number because it is a ratio of whole numbers.

The number, $\pi$ , on the other hand, is irrational, since it has an irregular sequence of numbers ( 3.14159 ...) that cannot be written as a fraction.

Report an Error

View Algebra 2 Tutors

Chelsea
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Physics. The University of Texas at Dallas, Master of Science, Bioinf...

View Algebra 2 Tutors

Ataul
Certified Tutor

Temple University, Bachelor of Science, Financial Planning.

View Algebra 2 Tutors

Mariam
Certified Tutor

Yarmouk University, Bachelor of Science, Mathematics. Touro College, Master of Science, Teacher Education, Multiple Levels.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in San Diego, Physics Tutors in Atlanta, Spanish Tutors in Denver, SSAT Tutors in Dallas Fort Worth, Physics Tutors in Los Angeles, GRE Tutors in Seattle, Math Tutors in Washington DC, Biology Tutors in Los Angeles, ISEE Tutors in Dallas Fort Worth, Statistics Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Boston, SAT Courses & Classes in Phoenix, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Seattle, ACT Courses & Classes in New York City, SAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Seattle

Popular Test Prep

ACT Test Prep in Phoenix, GRE Test Prep in Los Angeles, SSAT Test Prep in Miami, MCAT Test Prep in Washington DC, ISEE Test Prep in Denver, LSAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Phoenix, LSAT Test Prep in Washington DC, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Irrational Numbers

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #5123 : Algebra Ii

Which of the below is NOT an irrational number?

Example Question #32 : Irrational Numbers

Example Question #5124 : Algebra Ii

Example Question #5125 : Algebra Ii

Example Question #5126 : Algebra Ii

Example Question #5127 : Algebra Ii

Example Question #1 : Irrational Numbers

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: