All Algebra II Resources
Example Questions
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
For the function 
End Behavior: As 
Local maxima and minima: (0, 1) and (2, -3)
Symmetry: Neither even nor odd
End Behavior: As 
Local maxima and minima: (0, 1) and (2, -3)
Symmetry: Neither even nor odd
End Behavior: As 
Local maxima and minima: (0, -1) and (-2, 3)
Symmetry: Neither even nor odd
End Behavior: As 
Local maxima and minima: (0, -1) and (-2, 3)
Symmetry: Neither even nor odd
End Behavior: As 
Local maxima and minima: (0, 1) and (2, -3)
Symmetry: Neither even nor odd
To get started on this problem, it helps to use a graphing calculator or other graphing tool to visualize the function. The graph of 

When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Next, look at x=2, then x=3, and so on, and you can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 

Next, the question asks to identify any local minima and maxima. It helps to think of these as "peaks" and "valleys." Looking at the graph, it appears that these exist at the points (0, 1) and (2, -3). We can check this algebraically by plugging in these x values and seeing that the associated y values come out of the function.
This confirms that the point (0, 1) is a local maxima (peak) and the point (2, -3) is a local minima (valley).
Finally, the question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. The right side of this graph has a local minima, while the left side does not, therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does not, therefore, the graph has no symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x).
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of

Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Odd symmetry
No symmetry
Even symmetry
Even symmetry
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. We can see that what is on the left side of the line x=0 is an exact match of what is on the right side of the line x=0. Therefore, this graph has even symmetry. Algebraically, a function has even symmetry if f(x)=f(-x). You can plug in several test values of x to see this for yourself.
Example Question #612 : Functions And Graphs
Below is the graph of

Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting bigger and bigger (more and more positive.) Therefore, as x approaches negative infinity, y approaches infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 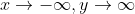

Example Question #5152 : Algebra Ii
Below is the graph of

Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting bigger and bigger (more and more positive.) Therefore, as x approaches negative infinity, y approaches infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, y gets more and more negative. Therefore as x approaches infinity, y approaches negative infinity. Mathematically, this is written like:
As 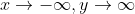

Example Question #614 : Functions And Graphs
Below is the graph of

Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 

Example Question #2 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of

Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph does not have any symmetry.
This graph has even symmetry.
This graph has odd symmetry.
This graph has odd symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph, while Quadrant II (x negative, y positive) has no part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
Example Question #5154 : Algebra Ii
Below is the graph of

Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph has even symmetry.
This graph has no symmetry.
This graph has odd symmetry.
This graph has no symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph as does Quadrant II (x negative, y positive); however, these pieces are not mirror images of one another. Therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. In the original graph, the graph flattens above the origin, but if we flip this upside down, it flattens below the origin. While it has odd symmetry around the point (0, 5), it does not have symmetry around the origin, and therefore the function is not odd. Therefore, this graph does not have symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see that neither of these are satisfied.
Example Question #2 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of

Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 

Example Question #3 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of

Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph has even symmetry.
This graph has odd symmetry.
This graph has no symmetry.
This graph has odd symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has no piece of this graph, while Quadrant II (x negative, y positive) has a part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
All Algebra II Resources



































