All Algebra II Resources
Example Questions
Example Question #5 : Percentiles

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the 
The stem-and-leaf display represents 53 scores. The score at the 35th percentile would be the score that is greater than 35% of the scores, or

Rounding, we count 19 scores from the bottom:

The score represented is 64, which is the correct response.
Example Question #1 : Variance
Calculate the variance of the following set of values.
Variance is the average of the squared differences from the mean. So start by working out the mean of the set of values.
Then, for each number, subtract the mean and square the result.
The average of the results is the variance.
Example Question #2 : Variance
What is the variance of the following set of numbers?
Remember that the variance of a set of numbers is equal to its standard deviation squared. So if the formula for standard deviation is known to be:
Then the variance is simply 
Where 


We then find each value that will be added together by subtracting our mean from each of the numbers in our set and then squaring the result:
Looking at our formula for variance, all we must do now is add these values together and divide by N:
Example Question #3 : Variance
A set of five numbers is given as follows, where one of the numbers, 
If the mean of the set is 
Before we can determine the variance of the set, we must first determine the value of x, our unknown. The problem tells us the mean of the set, and we know each number in the set except for x, so we can solve for x as follows:
Now that we know all the values of the set, the mean, and the number of values, we can solve for the variance using the following equation:
Where 


Now that we now each value of the summation, all we have left to do is add them all together and divide the final result by N:
Example Question #2 : Deviation Concepts
What is the variance for the values 


Write the formula for variance.
The value of 
The value of 
Find the mean, 
Rewrite the variance formula:
Example Question #3 : Deviation Concepts
Determine the variance if the standard deviation is 
Write the formula relationship between standard deviation and variance.
The standard deviation is the square root of variance.
Substitute the standard deviation.
Square both sides.
The answer is:
Example Question #4 : Deviation Concepts
Evaluate the variance if the standard deviation is 
Write the formula for the variance.
The standard deviation is the square root of variance.
Substitute the value of standard deviation in the formula.
Square both sides.
The answer is:
Example Question #1 : Variance
The standard deviation of a distribution is 9. What is the variance?
The variance of a distribution is equal to the standard deviation squared.
Example Question #6 : Deviation Concepts
Determine the population variance given the following data set:
To determine the variance, we will need to find the squared differences of the mean, and take the average.
Find the mean.
Subtract each number from the mean and square the quantities.
Divide this value by three.
The answer is:
Example Question #1 : Standard Deviation
Calculate the standard deviation of the following set of values.
To get the standard deviation, we need to calculate the variance, which is the average of the squared differences from the mean, so we will start by getting the mean.
Then, subtract the mean from each value...
...and take the mean of these resulting values, which is equal to the variance.
The square root of this value is the standard deviation. The answer is presented as 
but you may also calculate it and find it equal to about
All Algebra II Resources






















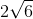

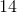




























































![[5,7,27]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/861647/gif.latex)



























