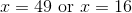We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #48 : Radicals And Fractions

Solve the radical: $\frac{\sqrt{3}\times \sqrt{5}}{\sqrt{32}}$

Possible Answers:

$\frac{\sqrt{30}}{4}$

$\frac{2\sqrt{15}}{3}$

$\frac{\sqrt{15}}{8}$

$\frac{\sqrt{30}}{8}$

$\frac{\sqrt{15}}{4}$

Correct answer:

$\frac{\sqrt{30}}{8}$

Explanation:

Simplify the top of the fraction.

$\frac{\sqrt{3}\times \sqrt{5}}{\sqrt{32}}=\frac{\sqrt{15}}{\sqrt{32}}$

We can simplify the denominator first.

$\sqrt{32} = \sqrt{16}\times \sqrt2 =4\sqrt2$

Rationalize the denominator by multiplying the top and bottom of the fraction by the radical. Simplify the radicals.

$\frac{\sqrt{15}}{4\sqrt2}\cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{30}}{4 \times 2}= \frac{\sqrt{30}}{8}$

The answer is: $\frac{\sqrt{30}}{8}$

Report an Error

Example Question #49 : Radicals And Fractions

Simplify: $\frac{4\sqrt{8}}{5\sqrt{3}}$

Possible Answers:

$\frac{\sqrt{6}}{6}$

$\frac{3\sqrt{6}}{4}$

$\frac{2\sqrt{6}}{5}$

$\frac{4\sqrt{3}}{5}$

$\frac{8\sqrt{6}}{15}$

Correct answer:

$\frac{8\sqrt{6}}{15}$

Explanation:

Rationalize the denominator by multiplying both the top and bottom by the denominator.

$\frac{4\sqrt{8}}{5\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{4\sqrt{24}}{5\times3} = \frac{4\sqrt{4}\times \sqrt{6}}{15}=\frac{4(2)\times \sqrt{6}}{15}$

The answer is: $\frac{8\sqrt{6}}{15}$

Report an Error

Example Question #1551 : Mathematical Relationships And Basic Graphs

Simplify: $\frac{7\sqrt7}{\sqrt{\frac{1}{7}}}$

Possible Answers:

$\sqrt{14}$

$\frac{1}{7}$

$\frac{1}{49}$

Correct answer:

Explanation:

The radical $\sqrt{\frac{1}{7}}$ can be rewritten as:

$\frac{\sqrt1}{\sqrt7} = \frac{1}{\sqrt7}$

Rationalize the denominator by multiplying both the top and bottom by the denominator.

$\frac{1}{\sqrt7} \cdot \frac{\sqrt7}{\sqrt7} =\frac{\sqrt7}{7}$

Rewrite the given question.

$\frac{7\sqrt7}{\sqrt{\frac{1}{7}}} = \frac{7\sqrt7}{\frac{\sqrt7}{7}}$

Simplify this complex fraction by rewriting it as a division sign.

$\frac{7\sqrt7}{\frac{\sqrt7}{7}} = 7\sqrt7 \div \frac{\sqrt7}{7}$

Change the division sign to multiplication and take the reciprocal of the second term.

$7\sqrt7 \div \frac{\sqrt7}{7} = 7\sqrt7 \times \frac{7}{\sqrt7} =49$

The answer is:

Report an Error

Example Question #4211 : Algebra Ii

Rationalize: $\frac{9}{\sqrt{20}}$

Possible Answers:

$\frac{3\sqrt{2}}{4}$

$\frac{9\sqrt{2}}{4}$

$\frac{3\sqrt{5}}{10}$

$\frac{9\sqrt{5}}{10}$

$\frac{3\sqrt{2}}{2}$

Correct answer:

$\frac{9\sqrt{5}}{10}$

Explanation:

We can factor the square root twenty before rationalizing the value so that the final term would not be as difficult to factor.

Factor $\sqrt{20}$ using factors of perfect squares.

$\sqrt{20}= \sqrt{4}\times \sqrt5 = 2\sqrt5$

The expression becomes:

$\frac{9}{\sqrt{20}} = \frac{9}{2\sqrt{5}}$

Instead of multiplying $\sqrt{20}$ on both the top and bottom, we will multiply $\sqrt5$ on the top and bottom.

$\frac{9}{2\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{9\sqrt{5}}{10}$

The answer is: $\frac{9\sqrt{5}}{10}$

Report an Error

Example Question #222 : Simplifying Radicals

Try without a calculator.

Simplify:

$\sqrt{\frac{5}{8}}$

Possible Answers:

$\frac{\sqrt{10}}{2}$

$\frac{\sqrt{5}}{2}$

$\frac{\sqrt{10}}{4}$

None of the other choices gives the correct response.

$\frac{\sqrt{5}}{4}$

Correct answer:

$\frac{\sqrt{10}}{4}$

Explanation:

First, apply the Quotient of Radicals Property to split the radical into a numerator and a denominator:

$\sqrt{\frac{5}{8}}$

$= \frac{\sqrt{5}}{\sqrt{8}}$

Simplify the denominator by applying the Product of Radicals Property, as follows:

$= \frac{\sqrt{5}}{\sqrt{4} \cdot \sqrt{2}}$

$= \frac{\sqrt{5}}{2\cdot \sqrt{2}}$

Rationalize the denominator by multiplying both halves of the fraction by $\sqrt{2}$ :

$= \frac{\sqrt{5} \cdot \sqrt{2}}{2\cdot \sqrt{2} \cdot \sqrt{2}}$

Apply the Product of Radicals property in the numerator:

$= \frac{\sqrt{5 \cdot 2}}{2\cdot 2}$

$= \frac{\sqrt{10}}{4}$ ,

the correct response.

Report an Error

Example Question #4212 : Algebra Ii

Try without a calculator.

Simplify:

$\sqrt{\frac{12}{7}}$

Possible Answers:

$\frac{3\sqrt{14} }{7}$

None of these

$\frac{ \sqrt{42} }{7}$

$\frac{2 \sqrt{21} }{7}$

$\frac{6\sqrt{7} }{7}$

Correct answer:

$\frac{2 \sqrt{21} }{7}$

Explanation:

First, apply the Quotient of Radicals Property to split the radical into a numerator and a denominator:

$\sqrt{\frac{12}{7}}$

$= \frac{\sqrt{12}}{\sqrt{7}}$

Simplify the numerator by applying the Product of Radicals Property, as follows:

$\frac{\sqrt{4 \cdot 3 }}{\sqrt{7}}$

$= \frac{\sqrt{4} \cdot \sqrt{3}}{\sqrt{7}}$

$= \frac{2 \sqrt{3}}{\sqrt{7}}$

Rationalize the denominator by multiplying both halves of the fraction by $\sqrt{7}$ :

$\frac{2 \sqrt{3} \cdot \sqrt{7} }{\sqrt{7} \cdot \sqrt{7}}$

Apply the Product of Radicals Property in the numerator:

$\frac{2 \sqrt{3 \cdot 7} }{7}$

$= \frac{2 \sqrt{21} }{7}$

Report an Error

Example Question #1 : Solving And Graphing Radicals

Solve for :

$x + 3 \sqrt{x} = 28$

Possible Answers:

$x = -49 \textup{ or }x = 16$

$x = - \sqrt{7} \textup{ or }x = 2$

None of the other responses is correct.

$x = 49 \textup{ or }x = 16$

$x = i \sqrt{7} \textup{ or }x = 2$

Correct answer:

None of the other responses is correct.

Explanation:

One way to solve this equation is to substitute for $\sqrt{x}$ and, subsequently, $u^{2}$ for :

$x + 3 \sqrt{x} = 28$

$u^{2} + 3 u = 28$

$u^{2} + 3 u - 28 = 0$

Solve the resulting quadratic equation by factoring the expression:

(u+7)(u-4) = 0

Set each linear binomial to sero and solve:

u + 7 = 0

u = -7

u - 4 = 0

u = 4

Substitute back:

u = -7

$\sqrt{x}= -7$ - this is not possible.

u = 4

$\sqrt{x}= 4$

x = 16 - this is the only solution.

None of the responses state that x = 16 is the only solution.

Report an Error

Example Question #1 : Solving Radical Equations

Solve the following radical equation.

$\frac{10\sqrt{8}}{\sqrt{16}} + 3\sqrt{2}$

Possible Answers:

$13\sqrt{2}$

$8\sqrt{2}$

$\frac{10}{\sqrt{2} } +3\sqrt{2}$

$5\sqrt{8} + 3\sqrt{2}$

Correct answer:

$8\sqrt{2}$

Explanation:

We can simplify the fraction:

$\frac{10\sqrt{8}}{\sqrt{16}} = \frac{10\sqrt{4\times 2}}{4}=\frac{10(2\sqrt{2})}{4} =\frac{20\sqrt{2}}{4}=5\sqrt{2}$

Plugging this into the equation leaves us with:

$5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}$

Note: Because they are like terms, we can add them.

Report an Error

Example Question #3 : Solving Radical Equations

Solve the following radical equation.

$\sqrt{x-6} =2$

Possible Answers:

$x=6 +\sqrt{2}$

x=2

x=-10

x=10

Correct answer:

x=10

Explanation:

In order to solve this equation, we need to know that

$(\sqrt{x-6})^{2} = x-6$

How? Because of these two facts:

$\sqrt{x-6} = (x-6)^{\frac{1}{2}}$
Power rule of exponents: when we raise a power to a power, we need to mulitply the exponents:

$\frac{1}{2} \times2=1$

With this in mind, we can solve the equation:

$\sqrt{x-6} =2$

In order to eliminate the radical, we have to square it. What we do on one side, we must do on the other.

$(\sqrt{x-6})^{2} = 2^{2}$

x-6=4

x=10

Report an Error

Example Question #4 : Solving Radical Equations

Solve the following radical equation.

$\sqrt{\frac{x}{2}}=5$

Possible Answers:

x=10

x=50

$x=2\sqrt{5}$

$x=\sqrt{10}$

Correct answer:

x=50

Explanation:

In order to solve this equation, we need to know that

$\bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =\frac{x}{2}$

Note: This is due to the power rule of exponents.

With this in mind, we can solve the equation:

$\sqrt{\frac{x}{2}} =5$

In order to get rid of the radical we square it. Remember what we do on one side, we must do on the other.

$\bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =5^{2}$

$\frac{x}{2} =25$

$\frac{2}{1} \bigg(\frac{x}{2}\bigg)=25\bigg(\frac{2}{1}\bigg)$

x=50

Report an Error

View Algebra 2 Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

View Algebra 2 Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

View Algebra 2 Tutors

Saarim
Certified Tutor

St Edwards University, Bachelor of Science, Mathematics.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Washington DC, ISEE Tutors in Dallas Fort Worth, Calculus Tutors in Dallas Fort Worth, ISEE Tutors in Denver, Spanish Tutors in Philadelphia, Chemistry Tutors in Atlanta, Biology Tutors in Washington DC, SAT Tutors in Los Angeles, Statistics Tutors in Philadelphia, Calculus Tutors in San Diego

Popular Courses & Classes

SSAT Courses & Classes in Washington DC, SSAT Courses & Classes in Atlanta, SSAT Courses & Classes in New York City, LSAT Courses & Classes in San Diego, SAT Courses & Classes in Boston, GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Miami, ISEE Courses & Classes in Phoenix, SSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Chicago, LSAT Test Prep in Washington DC, ISEE Test Prep in Chicago, SAT Test Prep in Denver, LSAT Test Prep in Denver, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Los Angeles, LSAT Test Prep in Los Angeles, GRE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #48 : Radicals And Fractions

Example Question #49 : Radicals And Fractions

Example Question #1551 : Mathematical Relationships And Basic Graphs

Example Question #4211 : Algebra Ii

Example Question #222 : Simplifying Radicals

Example Question #4212 : Algebra Ii

Example Question #1 : Solving And Graphing Radicals

Example Question #1 : Solving Radical Equations

Example Question #3 : Solving Radical Equations

Example Question #4 : Solving Radical Equations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: