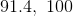Part 1: Finding the mean (average)

We must find the average Elo rating of the players competing at this tournament. The way to calculate the mean is to add up all of the values, and then to divide that number by the amount of values.

In other words, we must take                                                                    

and divide that by the total number of players (6). 

When you type this into your calculator, you may get a number that is approximately  with the  repeating infinitely. 

Part 2: Rounding

The problem asks us to round to the nearest whole number.

 can be rounded to . 

Solution: 

The mean is the average of all of the numbers, so

,

and

. 

If we assign our sixth and final score a variable, let's say , we can use the formula for the mean: 

.

Remember to divide by 6 instead of 5 because we have now added in a sixth score. From here, we would multiply both sides by 6 to get rid of the denominator on the left side, leaving us with 

.

Solving, we get .

To calculate this, you need to figure out the total number of inches in the classroom. This is calculated by multiplying each group by its average number of inches. For the girls, there will be 30 after they double. Their total number of inches can be found by multiplying the average height by 30:

The boys' total height can be found by multiplying their average by 30 as well:

There are now 60 students total, so the average number of inches is the combined height of the boys and girls divided by 60:

The averge height in the class is 45.25 inches.

The mean is just the average of all the test scores, which is found by adding up the scores and dividing by the number of scores ().  This gives  as the mean.  The mode is the score which occurs most frequently.  In this case, the mode is .  The median, the middle score of the sequence, is .

Let's think of this list of numbers:

2, 4, 6, ...

Where does it end? The first 5 even numbers goes to 10. That means that the last number in the first 20 will be the number 40. So the question is, "Where is the middle?" Well, this is an even number of values, so there is no actual middle. What we have to do, then is find the 10th and the 11th numbers and take their average. The 10th number is easy, based on what we just said. If the 5th is 10, then the 10th is 20. The 11th will just be two more than that, namely 22. To calculate the median, we just have to find the average of those two numbers:

If you prefer to write out the full list:

2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40

To answer this question, you need to know the first ten prime numbers! Remember, prime numbers are all of the integers that are divisible only by themselves and by 1.  They do not include 1.  So, our list is:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

The median is the "middle value." There is no proper "middle" since we have an even number of values. We need to take the 5th and the 6th elements (the middle two values) and average them. The 5th term is 11 and the 6th is 13; therefore, the median is:

The first thing to do is figure out which stalk is in the "middle." Since there are an even number of stalks, there is no exact middle; there are 500 on one side and 500 on the other. This means that the 500th and the 501st are the median. These will have to be averaged.

Now, we need to determine the height of these two stalks. Consider the pattern given:

1st stalk: 10 feet

2nd stalk: 20 feet

3rd stalk: 30 feet

4th stalk: 40 feet

You should see the pattern that emerges for this problem. Each stalk is 10 times that stalk's place in the row. This means that the 500th stalk will be:

The 501st stalk will be:

The average of these two numbers is:

5005 feet is the median.

The median in a data set is the number that lies directly in the middle. To determine the median, first list the numbers in ascending order:

Then, count in from both sides to find the number that lies directly in the middle. Therefore the correct answer is "median".

Reorder the numbers in ascending order (from lowest to highest):

11, 13, 13, 13, 13, 14, 16, 19

Find the middle number. In this case, the middle number is the average of the 4th and 5th numbers. Because both the 4th and 5th number are 13, the answer is simply 13.