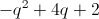Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #141 : Variables

Simplify the following:

n(n+1) -n(n+2)

Possible Answers:

-n^2-3n

n^2-3n

n^2-3

-n^2+3n

Correct answer:

Explanation:

To solve this problem, first distribute anything through parentheses that needs to be distributed, then combine all terms with like variables (i.e. same variable, same exponent):

Report an Error

Example Question #32 : How To Subtract Polynomials

Subtract the polynomials 2x^2-3x+6 and 3x^2-6x+3 .

Possible Answers:

-x^2-9x-9

-x^2-9x+9

-x^2+3x+3

-x^2+3x-3

-x^2-3x-3

Correct answer:

-x^2+3x+3

Explanation:

Write the problem as an expression. Remember to brace both polynomials with parentheses since we are subtracting by the quantity.

(2x^2-3x+6)-(3x^2-6x+3)

Remove the parentheses. Simplify by distributing the negative sign through the second polynomial.

2x^2-3x+6-3x^2+6x-3

Combine like-terms.

The answer is: -x^2+3x+3

Report an Error

Example Question #33 : How To Subtract Polynomials

Subtract the polynomials 3x^2-3x-6 and -2x^2-x-3

Possible Answers:

5x^2-2x-3

x^2-2x-9

5x^2-4x-9

5x^2-4x-3

x^2-4x-9

Correct answer:

5x^2-2x-3

Explanation:

Set up an expression and enclose both polynomials with parentheses.

(3x^2-3x-6)-(-2x^2-x-3)

Remove the parentheses and distribute the negative sign through each term in the second polynomial.

3x^2-3x-6+2x^2+x+3

Combine like-terms.

The answer is: 5x^2-2x-3

Report an Error

Example Question #35 : How To Subtract Polynomials

Translate and simplify:

The sum of

$\left (x^{3}-2x^{2}+3x -5 \right )$

and $\left ( -2x^{3}-5x^{2}+9 \right )$

subtracted from

$\left ( -3x^{3}+5x^{2} -7x+15\right )$ .

Possible Answers:

$-6x^{3}+2x^{2}-10x+29$

$2x^{3}-12x^{2}+10x-11$

$-2x^{3}+12x^{2}-10x+11$

$-2x^{3}+2x^{2}-10x+11$

$2x^{3}-2x^{2}+10x-11$

Correct answer:

$-2x^{3}+12x^{2}-10x+11$

Explanation:

Sum the first two expressions:

$\left ( x^{3}-2x^{2}+3x -5 \right )$

$+\left ( -2x^{3}-5x^{2}+9 \right )$

$=-x^{3}-7x^{2}+3x+4$

Subtract the sum from $-3x^{3}+5x^{2}-7x +15$ to get:

$-3x^{3}+5x^{2}-7x+15 -( -x^{3}-7x^{2}+3x+4)$

By combining like terms we get:

$-2x^{3}+12x^{2}-10x +11$

Report an Error

Example Question #61 : Expressions

Simplify the following expression:

$(2q^{2}+4q+7)-(3q^{2}-5)$

Possible Answers:

$-3q^{2}+12$

$-q^{2}+4q+12$

$-5q^{2}+4q+2$

-q^2+4q+2

Correct answer:

$-q^{2}+4q+12$

Explanation:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms together:

$2q^{2}-3q^{2}=-1q^{2}=-q^2$

has no like terms.

7-(-5)=12

Combine these terms into one expression to find the answer:

$-q^{2}+4q+12$

Report an Error

Example Question #1 : How To Add Polynomials

Subtract $\left ( -3x^{3}+2x^{2}-xy -13 \right )$ from $\left ( x^{5}-4x^{4}-2x^{3}-9xy \right )$ .

Possible Answers:

$x^{5}-4x^{4}+x^{3}-2x^{2}-8xy +13$

$x^{5}+4x^{4}+x^{3}+2x^{2}-8xy-13$

$x^{5}-4x^{4}-5x^{3}-2x^{2}-10xy-13$

$x^{5}-4x^{4}+x^{3}-2x^{2}+13$

$x^{5}-4x^{4}+x^{3}-8xy-13$

Correct answer:

$x^{5}-4x^{4}+x^{3}-2x^{2}-8xy +13$

Explanation:

Subtract the first expression from the second to get the following:

$x^{5}-4x^{4}-2x^{3}-9xy - \left ( -3x^{3}+2x^{2}-xy -13 \right )$

This is equal to:

$x^{5}-4x^{4}-2x^{3}-9xy+3x^{3}-2x^{2}+xy+13$

Combine like terrms:

$x^{5}-4x^{4}+x^{3}-2x^{2}-8xy+13$

Report an Error

Example Question #1 : How To Add Polynomials

Simplify the following: (x^2+3.5x+10)-(5x^2-1.5x+2)

Possible Answers:

-4x^2+2x+8

6x^2+5x+8

6x^2+2x+8

-4x^2+5x+8

Correct answer:

-4x^2+5x+8

Explanation:

(x^2+3.5x+10)-(5x^2-1.5x+2)=x^2+3.5x+10-5x^2+1.5x-2

=x^2-5x^2+3.5x+1.5x+10-2=-4x^2+5x+8

Report an Error

Example Question #1932 : Algebra Ii

Simplify x(4 – x) – x(3 – x).

Possible Answers:

x²

Correct answer:

Explanation:

You must multiply out the first set of parenthesis (distribute) and you get 4x – x². Then multiply out the second set and you get –3x + x². Combine like terms and you get x.

x(4 – x) – x(3 – x)

4x – x² – x(3 – x)

4x – x² – (3x – x²)

4x – x² – 3x + x² = x

Report an Error

Example Question #1 : Polynomials

Simplify the following expression.

$(3p^{2}+8)+(-p^{2}+5)$

Possible Answers:

$-3p^{2}+13$

$2p^{2}+13$

$-3p^{2}+40$

$-3p^{2}-3$

$2p^{2}+3$

Correct answer:

$2p^{2}+13$

Explanation:

$(3p^{2}+8)+(-p^{2}+5)$

This is not a FOIL problem, as we are adding rather than multiplying the terms in parenteses.

Add like terms to solve.

$3p^{2}-p^{2}=2p^{2}$

8+5=13

Combining these terms into an expression gives us our answer.

$2p^{2}+13$

Report an Error

Example Question #2 : How To Add Polynomials

Simplify the expression.

$15x^{3}y^{2}+8x^{2}+3x^{3}y^{2}-4x^{2}$

Possible Answers:

None of the other answers are correct.

$22x^{6}y^{4}$

$18x^{3}y^{2}-4x^{2}$

$18x^{3}y^{2}+4x^{2}$

$22x^3y^{2}x^{2}$

Correct answer:

$18x^{3}y^{2}+4x^{2}$

Explanation:

When simplifying polynomials, only combine the variables with like terms.

$15x^{3}y^{2}$ can be added to $3x^{3}y^{2}$ , giving $18x^{3}y^{2}$ .

$4x^{2}$ can be subtracted from $8x^{2}$ to give $4x^{2}$ .

Combine both of the terms into one expression to find the answer: $18x^{3}y^{2}+4x^{2}$

Report an Error

View Algebra Tutors

Sydni
Certified Tutor

Louisiana Tech University, Bachelor of Science, Finance. Louisiana Tech University, Master of Arts Teaching, Mathematics.

View Algebra Tutors

Masoud
Certified Tutor

University of Guilan,, Bachelor of Science, Biological/Biosystems Engineering. University of Tehran, Master of Science, Anima...

View Algebra Tutors

Allison
Certified Tutor

Asbury University, Bachelor of Education, Mathematics Teacher Education.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Philadelphia, GRE Tutors in Denver, English Tutors in Chicago, Spanish Tutors in Los Angeles, SAT Tutors in Phoenix, Math Tutors in Washington DC, Reading Tutors in San Diego, Spanish Tutors in New York City, Statistics Tutors in Chicago, MCAT Tutors in Washington DC

Popular Courses & Classes

GRE Courses & Classes in Seattle, Spanish Courses & Classes in Seattle, MCAT Courses & Classes in Boston, SAT Courses & Classes in New York City, SSAT Courses & Classes in Atlanta, GRE Courses & Classes in Boston, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, ACT Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Denver, LSAT Test Prep in Houston, SAT Test Prep in San Diego, MCAT Test Prep in Atlanta, ISEE Test Prep in San Diego, MCAT Test Prep in San Diego, GRE Test Prep in Miami, GMAT Test Prep in Atlanta, SAT Test Prep in Philadelphia, GMAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #141 : Variables

Example Question #32 : How To Subtract Polynomials

Example Question #33 : How To Subtract Polynomials

Example Question #35 : How To Subtract Polynomials

Example Question #61 : Expressions

Example Question #1 : How To Add Polynomials

Example Question #1 : How To Add Polynomials

Example Question #1932 : Algebra Ii

Example Question #1 : Polynomials

Example Question #2 : How To Add Polynomials

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: