Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : How to graph a quadratic function

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Parabolic Functions

What is the minimum possible value of the expression below?

$3x^{2}+6x-10$

Possible Answers:

The expression has no minimum value.

Correct answer:

Explanation:

We can determine the lowest possible value of the expression by finding the -coordinate of the vertex of the parabola graphed from the equation $y=3x^{2}+6x-10$ . This is done by rewriting the equation in vertex form.

$3x^{2}+6x-10$

$3(x^{2}+2x)-10$

$3(x^{2}+2x+1)-3* 1-10$

$3(x+1)^{2}-13$

The vertex of the parabola $y=3(x+1)^{2}-13$ is the point (-1, -13) .

The parabola is concave upward (its quadratic coefficient is positive), so represents the minimum value of . This is our answer.

Report an Error

Example Question #1 : Graphing Quadratic Functions

What is the vertex of the function $\small f(x)=2(x-4)^2+7$ ? Is it a maximum or minimum?

Possible Answers:

$\small (-4,7)$ ; maximum

$\small (4,7)$ ; minimum

$\small (4,7)$ ; maximum

$\small (-4,7)$ ; minimum

Correct answer:

$\small (4,7)$ ; minimum

Explanation:

The equation of a parabola can be written in vertex form: $\small f(x)=a(x-h)^2+k$ .

The point $\small (h,k)$ in this format is the vertex. If $\small a$ is a postive number the vertex is a minimum, and if $\small a$ is a negative number the vertex is a maximum.

$\small f(x)=2(x-4)^2+7$

In this example, $\small a=2$ . The positive value means the vertex is a minimum.

$\small h=4\ \text{and}\ k=7$

$\small (h,k)=(4,7)$

Report an Error

Example Question #1 : Graphing Polynomial Functions

Which of the graphs best represents the following function?

$f(x)=\frac{9}{10}x^2-7x+2$

Possible Answers:

Graph_cube_

Graph_line_

None of these

Graph_parabola_

Graph_exponential_

Correct answer:

Graph_parabola_

Explanation:

$f(x)=\frac{9}{10}x^2-7x+2$

The highest exponent of the variable term is two ( x^2 ). This tells that this function is quadratic, meaning that it is a parabola.

The graph below will be the answer, as it shows a parabolic curve.

Graph_parabola_

Report an Error

Example Question #1 : How To Graph A Quadratic Function

What is the equation of a parabola with vertex (4,1) and -intercept (0,-7) ?

Possible Answers:

$y = -\frac{1}{2} x^{2} +4x - 7$

$y = \frac{1}{2} x^{2} +8x - 7$

$y = \frac{1}{2} x^{2} -4x - 7$

$y = -\frac{1}{2} x^{2} -4x - 7$

$y = \frac{1}{2} x^{2} -8x - 7$

Correct answer:

$y = -\frac{1}{2} x^{2} +4x - 7$

Explanation:

From the vertex, we know that the equation of the parabola will take the form $y = a (x - 4) ^{2}+ 1$ for some .

To calculate that , we plug in the values from the other point we are given, x = 0, y=-7 , and solve for :

$y = a (x - 4)^{2} + 1$

$-7= a \cdot (0 - 4)^{2} + 1$

$-7= a \cdot (- 4)^{2} + 1$

-7= 16a + 1

16a = -8

$a = -\frac{1}{2}$

Now the equation is $y = -\frac{1}{2} (x - 4)^{2} + 1$ . This is not an answer choice, so we need to rewrite it in some way.

Expand the squared term:

$y = -\frac{1}{2} (x^{2} -8x + 16) + 1$

Distribute the fraction through the parentheses:

$y = -\frac{1}{2} x^{2} +4x - 8 + 1$

Combine like terms:

$y = -\frac{1}{2} x^{2} +4x - 7$

Report an Error

Example Question #1 : Graphing Polynomial Functions

Possible Answers:

$y = -(x-2)^{2} - 2$

$y = (x-2)^{2}$

$y = (x+3)^{2}$

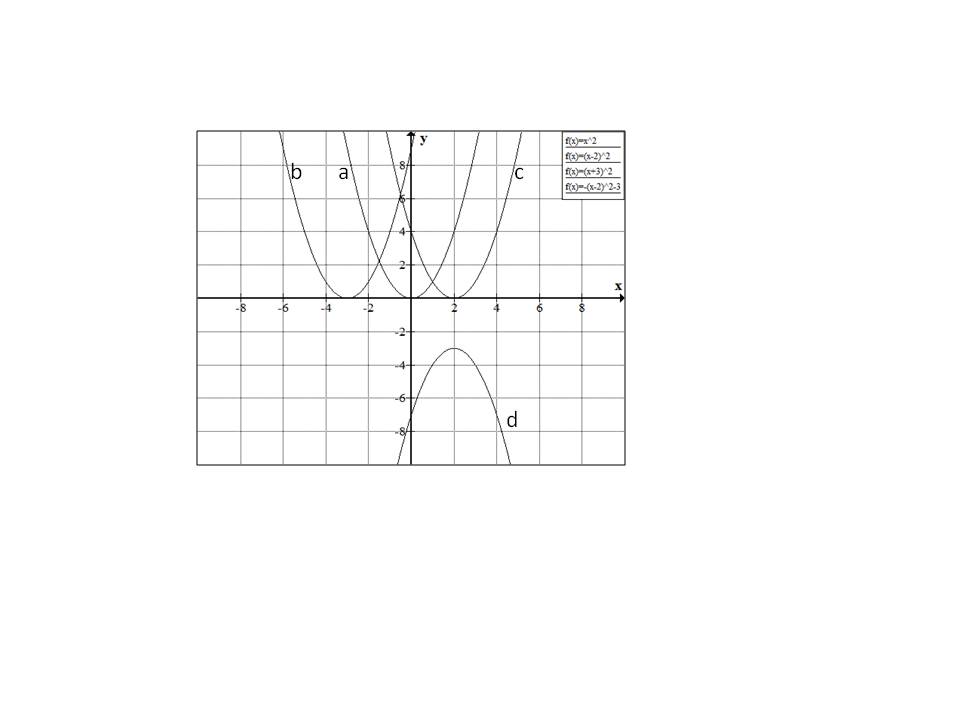
None of the above

$y = x^{2}$

Correct answer:

$y = (x+3)^{2}$

Explanation:

Starting with $y = x^{2}$

$(x-2)^{2}$ moves the parabola $x^{2}$ by units to the right.

Similarly $(x+3)^{2}$ moves the parabola by units to the left.

Hence the correct answer is option .

Report an Error

Example Question #21 : Quadratic Functions

Which of the following graphs matches the function y=(x-1)^2-2 ?

Possible Answers:

Graph

Graph4

Graph3

Graph1

Graph2

Correct answer:

Graph

Explanation:

Start by visualizing the graph associated with the function :

Graph5

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of looks like this:

Graph6

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function :

Graph

Report an Error

View Algebra Tutors

Pankaj
Certified Tutor

national institute of technology, mizoram, Bachelor, electrical engineering.

View Algebra Tutors

Gary
Certified Tutor

SUNY at Albany, Bachelor of Science, Economics. Pace University-New York, Masters in Business Administration, Analysis and Fu...

View Algebra Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Seattle, Spanish Tutors in Los Angeles, ACT Tutors in New York City, Chemistry Tutors in Philadelphia, SAT Tutors in Chicago, Statistics Tutors in Dallas Fort Worth, SSAT Tutors in Denver, Calculus Tutors in Atlanta, Spanish Tutors in Washington DC, Reading Tutors in San Francisco-Bay Area

Popular Courses & Classes

SAT Courses & Classes in Boston, GMAT Courses & Classes in Boston, MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Philadelphia, GRE Courses & Classes in Los Angeles, SSAT Courses & Classes in Boston, ACT Courses & Classes in Miami, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Atlanta

Popular Test Prep

MCAT Test Prep in Philadelphia, GRE Test Prep in Los Angeles, SAT Test Prep in Washington DC, ACT Test Prep in New York City, GMAT Test Prep in Atlanta, GMAT Test Prep in Boston, ISEE Test Prep in San Diego, SAT Test Prep in Atlanta, MCAT Test Prep in Washington DC, SSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : How to graph a quadratic function

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : Parabolic Functions

Example Question #1 : Graphing Quadratic Functions

Example Question #1 : Graphing Polynomial Functions

Example Question #1 : How To Graph A Quadratic Function

Example Question #1 : Graphing Polynomial Functions

Example Question #21 : Quadratic Functions

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: