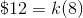Algebra 1 : Functions and Lines
Study concepts, example questions & explanations for Algebra 1
All Algebra 1 Resources
Example Questions
Example Question #211 : Functions And Lines
Does the equation below represent a direct variation? If it does, find the constant of variation.
No,
Yes,
Yes,
No,
Yes,
Yes,
Direct Variation is a relationship that can be represented by a function in the form
The equation is in the form 
The constant of variation or 
Therefore, the answer is,
Yes it is a direct variation, 
Example Question #212 : Functions And Lines
Suppose 
The general formula for direct proportionality is
where 
Solving for 
Example Question #5 : How To Find Direct Variation
The cost of a catering company varies directly with the number of people attending. If the cost is $100 when 20 people attend the party, find the constant of variation.
Because the cost varies directly with the number of people attending, we have the equation
Where 
We solve for 
And by dividing by 20 on both sides
Yields
Example Question #211 : Functions And Lines
The amount of money Billy earns is directly proportional to his hours worked. Suppose he earns 
Write the formula for direct proportionality.
Let:
Substitute twelve dollars and eight hours into this equation to solve for 
Divide by eight on both sides.
Substitute 
To find out the minimum number of hours Billy must work to make 
Multiply by two thirds on both sides.
Simplify both sides.
Billy must work at least 
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
The first term of an arithmetic sequence is 
To find the common difference 
For us, 
Now we can solve for 
Add the common difference to the first term to get the second term.
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
The sum of the first three terms of an arithmetic sequence is 111 and the fourth term is 49. What is the first term?
It cannot be determined from the information given.
Let 
The sum of the first three terms is 
Now we know that the second term is 37. The fourth term is the second term plus twice the common difference: 
The common difference is 6. The first term is 
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
An arithmetic sequence begins with 
For arithmetic sequences, we use the formula d "a_{n} = a_{1}+(n-1)d")
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
The fourth and tenth terms of an arithmetic sequence are 372 and 888, respectively. What is the first term?
Let 
Example Question #2 : How To Find The Nth Term Of An Arithmetic Sequence
The ninth and tenth terms of an arithmetic sequence are, respectively, 87 and 99. What is its first term?
The common difference of the sequence is the difference of the tenth and ninth terms: 
The ninth term of an arithmetic sequence with first term 
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
The eighth and tenth terms of an arithmetic sequence are, respectively, 87 and 99. What is its first term?
The eighth and tenth terms of the sequence are 
Now set eighth term 
Certified Tutor
Certified Tutor
All Algebra 1 Resources
