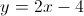We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Algebra 1

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Equations Of Lines

Give, in slope-intercept form, the equation of a line through the points (-2, 5) and (-3, 8) .

Possible Answers:

y = -3x -1

y = -3x -7

y = -3x +5

$y = -\frac{1}{3}x -\frac{1}{3}$

$y = -\frac{1}{3}x +8$

Correct answer:

y = -3x -1

Explanation:

First, use the slope formula to find the slope, setting $x_{1} = -2, y_{1} = 5,x_{2} = -3, y_{2} = 8$ .

$m = \frac{y _{2} - y_{1}}{x _{2} - x_{1}} = \frac{8 -5 }{-3-(-2)} = \frac{3 }{-1} = -3$

We can write the equation in slope-intercept form as

y = mx + b .

Replace m = -3 :

y = -3x + b

We can find by substituting for x,y using either point - we will choose (-2, 5) :

5= -3 (-2) + b

5= 6 + b

5-6 = 6 -6 + b

b = -1

The equation is y = -3x -1 .

Report an Error

Example Question #112 : Equations Of Lines

Give, in slope-intercept form, the equation of a line through the points $\left (3.5, 5.5 \right )$ and (5.5, -2.5) .

Possible Answers:

y = -0.25x + 5.5

y = -4x + 2.5

y = -4x + 3.5

y = -4x + 19.5

y = -0.25x + 13.5

Correct answer:

y = -4x + 19.5

Explanation:

First, use the slope formula to find the slope, setting $x_{1} = 3.5, y_{1} = 5.5,x_{2} = 5.5, y_{2} = -2.5$ .

$m = \frac{y _{2} - y_{1}}{x _{2} - x_{1}} = \frac{-2.5 -5.5}{5.5-3.5} = \frac{-8 }{2} = -4$

We can write the equation in slope-intercept form as

y = mx + b .

Replace m = -4 :

y = -4x + b

We can find by substituting for x,y using either point - we will choose (3.5, 5.5) :

5.5= -4 (3.5) + b

5.5= -14 +b

5.5+14 = -14 +14+b

b = 19.5

The equation is y = -4x + 19.5 .

Report an Error

Example Question #21 : How To Find The Equation Of A Line

Find the equation of the line that is parallel to y=3x+2 and contains the point (0,1).

Possible Answers:

$y=\frac{1}{3}x-1$

$y=\frac{-1}{3}x+1$

y=-3x-1

y=3x+1

Correct answer:

y=3x+1

Explanation:

To find the equation of a line, we need to know the slope and a point that passes through the line. We can then use the equation y-y_1=m(x-x_1) where m is the slope of the line, and $(x_{1}, y_{1})$ a point on the line. For parallel lines, the slopes are the same. The slope of y=3x+2 is 3, so the slope of the parallel line will be 3 as well. We know that the parallel line needs to contain the point (0,1), so we have all of the information we need. We can now use the equation $y-y_1=m(x-x_1)\Rightarrow y-1=3(x-0)\Rightarrow y=3x+1.$

Report an Error

Example Question #21 : Slope And Line Equations

Write an equation in the form y=mx+b for the line that fits the following points:

(4,3), (6,6), (10,12)

Possible Answers:

$y=-\frac{3}{2}x-6$

$y=\frac{2}{5}x-3$

y=3x-3

$y=\frac{5}{2}x-2$

$y=\frac{3}{2}x-3$

Correct answer:

$y=\frac{3}{2}x-3$

Explanation:

The equation of a line is written in the following format:

y=mx+b

1) The first step, then, is to find the slope, .

is equal to the change in divided by the change in .

So,

$\frac{6-3}{6-4}=\frac{3}{2}$

$y=\frac{3}{2}x+b$

2) Next step is to find . We can find values for and from any one of the given points, plug them in, and solve for .

Let's use (4,3)

So,

$3=\frac{3}{2}(4)+b$

3=6+b

b=-3

Then we just fill in our value for , and we have as a function of .

$y=\frac{3}{2}x-3$

Report an Error

Example Question #22 : Slope And Line Equations

Which of these lines has a slope of 4 and a y-intercept of 6?

Possible Answers:

None of the other answers

y=2x+3

y=4x+6

6y+4x=10

y=6x+4

Correct answer:

y=4x+6

Explanation:

When an equation is in the y=mx+b form, its slope is and its y-intercept is . Thus, we need an equation with an of 4 and a of 6, which would be

y=4x+6

Report an Error

Example Question #24 : How To Find The Equation Of A Line

Find the equation of the line with point $\left ( -5,3 \right )$ and slope of .

Possible Answers:

y=-4x+23

y=4x+23

y=4x-13

y=4x-23

Correct answer:

y=4x+23

Explanation:

Use the point-slope formula to find the equation:

$Y-Y_{1}=M(X-X_{1})$

y-3=4(x+5)

y-3 = 4x+20

y-3+3=4x+20+3

y=4x+23

Report an Error

Example Question #25 : How To Find The Equation Of A Line

Which of the following equations in standard form describes a line passing through the point $\left ( -2,5 \right )$ with a slope of $-3\ ?$

Possible Answers:

3x + y = 11

x + 3y = 6

-3x + y = 11

3x + y = - 1

-3x - 4y = - 1

Correct answer:

3x + y = - 1

Explanation:

Start by using point-slope form:

y-5 = -3 (x-(-2))

y-5 = -3(x+2)

Multiply the right side by the distributive property:

y-5 = -3x -6

Then, convert to standard form:

3x + y = - 1

Report an Error

Example Question #25 : How To Find The Equation Of A Line

Rewrite in slope-intercept form: 5x+20y=60 .

Possible Answers:

y=-4x+3

$y=\frac{1}{4}x+3$

$y=-\frac{1}{4}x+3$

y=4x+3

y=-4x-3

Correct answer:

$y=-\frac{1}{4}x+3$

Explanation:

Slope-intercept form is y=mx+b , where is the slope and is the y-intercept. To rewrite the original equation in slope-intercept form, you must isolate the variable:

5x+20y=60

-5x+20y=60-5x

20y=-5x+60

Now, divide each side by 20 so that stands alone and simplify, and you are left with the slope-intercept form of the equation:

$y=-\frac{5}{20}x+\frac{60}{20}$

$y=-\frac{1}{4}x+3$

Report an Error

Example Question #2 : Solving Linear Functions

Find the equation for the line goes through the two points below.

(1,-2)

(-3, 6)

Possible Answers:

$y = \frac{1}{2}x + 4$

y = 2x -4

y = 4x - 2

$y = \frac{1}{2}x$

y = -2x

Correct answer:

y = -2x

Explanation:

Let $P_{1} = (1, \; -2) \; \; and \; \; P_{2} = (-3, \; 6)$ .

First, calculate the slope between the two points.

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{6 - (-2)}{-3 - 1} = \frac{8}{-4} = -2$

Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for P_1 .

y = mx + b

-2 = -2(1) + b

b=0

Using slope-intercept form, where we know m=-2 and b=0 , we can see that the equation for this line is y = -2x .

Report an Error

Example Question #3641 : Algebra 1

What is the equation of the line connecting the points (-3,0) and (2,5) ?

Possible Answers:

y=x+3

y=x-3

y=3x+1

Equation is undefined or does not exist.

y=-x-3

Correct answer:

y=x+3

Explanation:

To find the equation of this line, we need to know its slope and y-intercept. Let's find the slope first using our general slope formula.

$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$

The points are and . In this case, our points are (–3,0) and (2,5). Therefore, we can calculate the slope as the following:

$m=\frac{5-0}{2-(-3)}=\frac{5}{5}=1$

Our slope is 1, so plug that into the equation of the line:

$y=mx+b \,\,\, \rightarrow \,\,\,y=(1)x+b \,\,\, \rightarrow \,\,\, y=x+b$

We still need to find b, the y-intercept. To find this, we pick one of our points (either (–3,0) or (2,5)) and plug it into our equation. We'll use (–3,0).

y=x+b

0=-3+b

Solve for b.

b=3

The equation is therefore written as y=x+3 .

Report an Error

View Algebra Tutors

Iman
Certified Tutor

Institut Américain Universitaire, Bachelor of Science, Electrical Engineering. Concordia University, Montreal, Master of Scie...

View Algebra Tutors

Matthew
Certified Tutor

Bluffton University, Bachelor of Education, Mathematics. Bluffton University, Masters in Education, Education.

View Algebra Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Seattle, GRE Tutors in Atlanta, ISEE Tutors in Boston, Algebra Tutors in San Diego, Chemistry Tutors in Los Angeles, Physics Tutors in Denver, GRE Tutors in Phoenix, Chemistry Tutors in Atlanta, GMAT Tutors in Houston, Reading Tutors in Chicago

Popular Courses & Classes

ACT Courses & Classes in Seattle, ACT Courses & Classes in Los Angeles, GMAT Courses & Classes in San Diego, ACT Courses & Classes in Boston, ACT Courses & Classes in Washington DC, GRE Courses & Classes in Denver, GRE Courses & Classes in Seattle, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Boston

Popular Test Prep

ISEE Test Prep in Houston, LSAT Test Prep in San Diego, LSAT Test Prep in Houston, SAT Test Prep in Chicago, SAT Test Prep in San Diego, GRE Test Prep in Chicago, ISEE Test Prep in Los Angeles, SAT Test Prep in San Francisco-Bay Area, ACT Test Prep in New York City, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Algebra 1

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #111 : Equations Of Lines

Example Question #112 : Equations Of Lines

Example Question #21 : How To Find The Equation Of A Line

Example Question #21 : Slope And Line Equations

Example Question #22 : Slope And Line Equations

Example Question #24 : How To Find The Equation Of A Line

Example Question #25 : How To Find The Equation Of A Line

Example Question #25 : How To Find The Equation Of A Line

Example Question #2 : Solving Linear Functions

Example Question #3641 : Algebra 1

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: