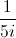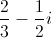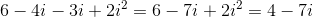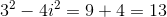Algebra 1 : Algebra 1
Study concepts, example questions & explanations for Algebra 1
All Algebra 1 Resources
Example Questions
Example Question #21 : How To Find Absolute Value
Solve the absolute value:
Compute the terms inside the absolute value first.
Any value inside the absolute value will be converted to a positive value.
Compute the square by order of operation.
Simplify this expression.
The answer is:
Example Question #3262 : Algebra 1
Solve the absolute value:
Solve the terms inside the absolute value first.
Simplify the absolute values.
Add the numbers.
The answer is:
Example Question #3263 : Algebra 1
Solve the absolute value:
Solve the terms inside the absolute value first.
A negative value inside the absolute value sign will be converted to a positive value.
Use order of operation to solve.
The answer is:
Example Question #3261 : Algebra 1
The symbol above represents the absolute value, which we find by simply determining the positive value of the number in question. If the number is positive, it remains positive, but if it is negative, we just drop the negative sign. Therefore, the absolute value of 
Example Question #1 : How To Graph An Inequality With A Number Line
Which line plot corresponds to the inequality below?
A closed circle indicates "greater than or equal to" or "less than or equal to," while and open circle indicates "greater than" or "less than". We can tell from the inequality that our line plot will only have closed circles, as the only symbol is "greater than or equal to."
Subtract 
Divide both sides by 
Our plot will show a closed circle on 
Example Question #1 : How To Graph An Inequality With A Number Line
What inequality is represented by the number line?
An open circle indictes "less than" or "greater than," while a closed circle indicates "greater than or equal to" or "less than or equal to".
This number line includes values that are less than 
Example Question #3262 : Algebra 1
Divide:
The answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
Example Question #3262 : Algebra 1
Solve the expression using the given values below.
We can simply plug in the values to each occurrence of the variables.
For 
Then 
Then 
Now we can solve.
Example Question #1 : How To Find The Number Of Integers Between Two Other Integers
What is the sum of the prime integers that satisfy the inequality 
The prime integers beterrn 20 and 40 are 23, 29, 31, and 37. Their sum is
Example Question #1 : How To Find The Number Of Integers Between Two Other Integers
What is the sum of all of the perfect squares and perfect cubes that satisfy the inequality 
There are four perfect squares between 10 and 50: 16, 25, 36, and 49. There is one perfect cube, 27, in this range. Add:
All Algebra 1 Resources
