All Advanced Geometry Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Rhombus






A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 

Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
Factoring,

The first solution is nonsensical for this problem.
Example Question #481 : Sat Subject Test In Math I




A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Using the Pythagorean Theorem,
Example Question #1 : Calculating The Length Of The Diagonal Of A Quadrilateral
Rhombus 
Which of the following could be true about the values of 

None of the other responses gives a correct answer.
The area of a rhombus is half the product of the lengths of its diagonals, which here are 

Therefore, we need to test each of the choices to find the pair of diagonal lengths for which this holds.

Area:
Area:
Area:
Area:

Example Question #51 : Rhombuses
Rhombus 


The sides of a rhombus are all congruent; since the perimeter of Rhombus 
The referenced rhombus, along with diagonal 

Since consecutive angles of a rhombus, as with any other parallelogram, are supplementary, 






Example Question #51 : Rhombuses
Rhombus 


The referenced rhombus, along with diagonals 

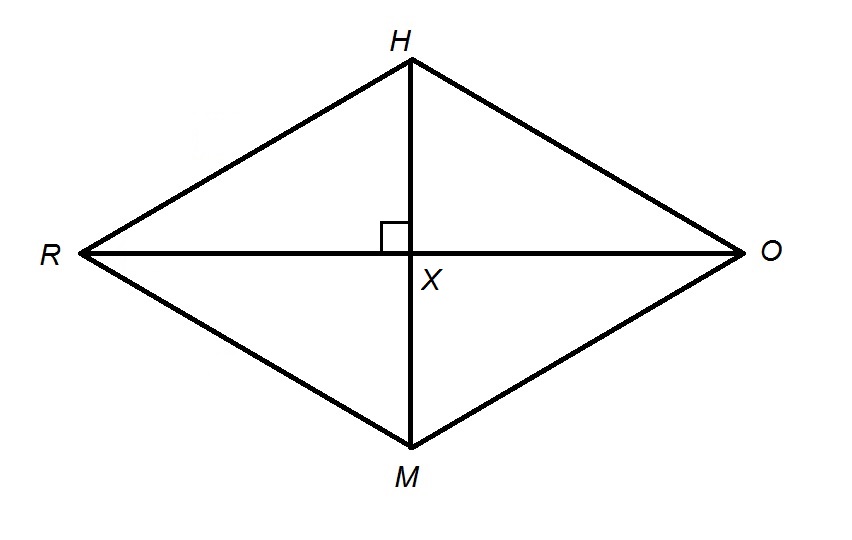
The four sides of a rhombus have equal measure, so each side has measure one fourth of the perimeter of 48, which is 12.
Since consecutive angles of a rhombus, as with any other parallelogram, are suplementary, 








and

Since the diagonals of a rhombus bisect each other, 
Example Question #51 : Rhombuses
If the area of a rhombus is 

Write the formula for the area of a rhombus.
Plug in the given area and diagonal length. Solve for the other diagonal.
Example Question #11 : How To Find The Length Of The Diagonal Of A Rhombus




Using the Law of Sines,
Example Question #61 : Rhombuses
Find the lengths of the two diagonals, the longer diagonal is 


1) All sides of a rhombus are congruent.
2) Because all sides of a rhombus are congruent, the expressions of the side lengths can be set equal to each other. The resulting equation is then solved,
3) Because the sides of a rhombus are congruent, 




4) Each of the composing triangles are right triangles, so then 
5) 
6) The standard 

7) The hypotenuse of a standard 

The result is 

8) For the standard 




9) The base of the triangle from step 7) is

and the height is

10) Diagonal

and diagonal

Example Question #441 : Advanced Geometry

What is the second diagonal for the above rhombus?
Because a rhombus has vertical and horizontal symmetry, it can be broken into four congruent triangles, each with a hypotenuse of 13 and a base of 5 (half the given diagonal).
The Pythagorean Theorem


The greater diagonal is twice the height of the triangles therefore, the greater diagonal becomes:
Example Question #11 : How To Find The Length Of The Diagonal Of A Rhombus





24
15
12
5
30
24
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,
Certified Tutor
Certified Tutor
All Advanced Geometry Resources