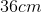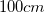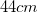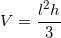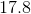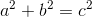All ACT Math Resources
Example Questions
Example Question #1 : Pyramids
A square pyramid has a volume of 
The formula for the volume of a pyramid is:
We know that 








This gives us a new equation of:
We then plug in the variables we know:
Multiply both sides by 3:
Divide both sides by 9:
Therefore, we now know that the length of the pyramid's base is 

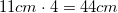

Example Question #2 : How To Find The Length Of An Edge Of A Pyramid
A square pyramid has a slant height of 8. The edge of a face is 12. What is the measure of an edge of its base?
In this kind of a problem, it's helpful to draw out all information that's given.
Because the triangular faces of a pyramid are isosceles triangles, the slant height can be seen to divide it into two right triangles. The goal is to find the measure of the edge of the square base. This quickly becomes a problem revolving around the use of the Pythagorean theorem.
If we take the measures 12 and 8 to be the hypotenuse and one of the legs, respectively, we can use the Pythagoream theorem to solve for the "base leg." Then, realizing that this measure if only half of the the total length of the square base edge, that value must be multiplied by 2.
Therefore,
Example Question #2 : Pyramids
What is the surface area of a square pyramid with a height of 12 in and a base side length of 10 in?
The surface area of a square pyramid can be broken into the area of the square base and the areas of the four triangluar sides. The area of a square is given by:
The area of a triangle is:
The given height of 12 in is from the vertex to the center of the base. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem:
where 

So, the area of the triangle is:
There are four triangular sides totaling 
The total surface area is thus 
Example Question #3 : Pyramids
Consider a square-base pyramid, 




The surface area of this pyramid is equal to the area of the square base plus the areas of each of the four triangular sides.
We are given the base and height of the triangular faces.
We can use 

Because the base of the triangular faces is equal to 3, we know the area of the square base is 
Therefore, our total surface area is equal to
Example Question #4 : Pyramids
The largest of the Great Egyptian Pyramids has a base length and width of 230 metrers and a height of 147 meters. What is the surface area of this rectangular pyramid in scientific notation?
The equation for surface area of a rectangular pyramid is as follows:
Plug in the values for length, width and height:
Example Question #53 : Solid Geometry
Find the surface of a isoceles pyramid whose height is 


To find surface area of a pyramid, simply find the surface area of each of the faces and add them together.
Since there are 4 trangular faces, we have to multiply that surface area by 4. Thus,
Example Question #5 : Pyramids
What is the sum of the number of vertices, edges, and faces of a square pyramid?
A square pyramid has one square base and four triangular sides.
Vertices (where two or more edges come together): 5. There are four vertices on the base (one at each corner of the square) and a fifth at the top of the pyramid.
Edges (where two faces come together): 8. There are four edges on the base (one along each side) and four more along the sides of the triangular faces extending from the corners of the base to the top vertex.
Faces (planar surfaces): 5. The base is one face, and there are four triangular faces that form the top of the pyramid.
Total
Example Question #1 : How To Find The Volume Of A Pyramid
An architect wants to make a square pyramid and fill it with 12,000 cubic feet of sand. If the base of the pyramid is 30 feet on each side, how tall does he need to make it?
Volume of Pyramid = 1/3 * Area of Base * Height
12,000 ft3 = 1/3 * 30ft * 30ft * H
12,000 = 300 * H
H = 12,000 / 300 = 40
H = 40 ft
Example Question #2 : How To Find The Volume Of A Pyramid



Find the volume of the pyramid:
The figure is not to scale.
A helpful strategy for this kind of a problem is to ask the following:
What information am I missing?
What information am I given?
Can I calculate for an unknown variable with the information I have?
The formula given is composed of the Base Area times the height of the pyramid times one-third. This means that in order to find the volume of this pyramid, the area of the square base must be calculated as well as the height of the pyramid (represented by the dashed line in the center). This will allow us to get an answer with cubed feet for units - an inkling that the volume was being calculated and not just the area. So the given equation may be expanded into: 
Calculating the base area:
Even though pyramids have a square base on which they're commonly seen to be standing on, the base area is calculated for the triangular face. Note that all the triangles are the same. 
Calculating the height of the pyramid:
The height of the pyramid is slightly more tricky than calculating B. Imagine creating a right triangle within the pyramid, which resembles a slpice from the exterior of one of the sides of the pyramid to the center, where the height would be measured. Such triangle is outlined by the dash marks in the following figure:
The hypotenuse of this triangle would be the height of the triangular face. The pyramid's height becomes to be one of the legs of the triangle - this is our unknown, and may be labeled as x. The other leg of the triangle is 5ft because the leg only extends the length of half of the base of one of the triangles (from one edge to the center).


Now all information may be substituted into the given equation to solve for the final volume:
Certified Tutor
Certified Tutor
All ACT Math Resources