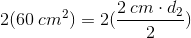Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Rhombuses

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 Next →

Example Question #11 : How To Find An Angle In A Rhombus

A rhombus has two interior angles each with a measurement of $46$^\circ$$ . Find the measurement for one of the two remaining angles.

Possible Answers:

$64$^\circ$$

$134$^\circ$$

$94$^\circ$$

$88$^\circ$$

$124$^\circ$$

Correct answer:

$134$^\circ$$

Explanation:

First, consider that the sum total of the four interior angles in any rhombus must equal $360$^\circ$$ . Secondly, a rhombus must have two sets of equivalent opposite interior angles, and a rhombus must have two sets of adjacent interior angles. The adjacent interior angles must be supplementary—meaning they have a sum total of $180$^\circ$$ .

One way to approach this problem is to realize that each of the remaining two angles must have the same measurement, and that each will be supplementary angles with $46$^\circ$$ . Therefore, find the difference between $180$^\circ$$ and $46$^\circ$$ to find the solution.

$180-46=134$^\circ$$

Report an Error

Example Question #12 : How To Find An Angle In A Rhombus

A rhombus has two interior angles each with a measurement of $159$^\circ$$ . Find the measurement for one of the two remaining angles.

Possible Answers:

$40$^\circ$$

$42$^\circ$$

$21$^\circ$$

$19$^\circ$$

$18$^\circ$$

Correct answer:

$21$^\circ$$

Explanation:

A rhombus must have two sets of equivalent opposite interior angles, and a rhombus must have two sets of adjacent interior angles. The adjacent interior angles must be supplementary—meaning they have a sum total of $180$^\circ$$ .

One way to approach this problem is to realize that each of the remaining two angles must have the same measurement, and that each will be supplementary angles with $159$^\circ$$ . Find the difference between $180$^\circ$$ and $159$^\circ$$ to find the solution.

$180-159=21$^\circ$$

Report an Error

Example Question #13 : How To Find An Angle In A Rhombus

A rhombus has two interior angles each with a measurement of $121$^\circ$$ . Find the sum of the remaining two angles.

Possible Answers:

$118$^\circ$$

$62$^\circ$$

$90$^\circ$$

$180$^\circ$$

$59$^\circ$$

Correct answer:

$118$^\circ$$

Explanation:

To solve this problem, consider that the sum total of the four interior angles in any rhombus must equal $360$^\circ$$ . Furthermore, a rhombus must have two sets of equivalent opposite interior angles, and a rhombus must have two sets of adjacent interior angles. The adjacent interior angles must be supplementary—meaning they have a sum total of $180$^\circ$$ .

Since this problem provides the measurement for two of the interior angles, find the sum of those two angles. Then subtract that sum from $360$^\circ$$ to find the sum of the two remaining interior angles.

The solution is:

121+121=242

$360-242=118$^\circ$$

Note: this means that each of the two remaining angles must have a measurement of $59$^\circ$$ .

Report an Error

Example Question #15 : How To Find The Length Of The Diagonal Of A Rhombus

If the area of a rhombus is $60\:cm^2$ , and the length of one of its diagonals is $2\:cm$ , what must be the length of the other diagonal?

Possible Answers:

$90\:cm$

$45\:cm$

$120\:cm$

$60\:cm$

$30\:cm$

Correct answer:

$60\:cm$

Explanation:

Write the formula for the area of a rhombus.

$A=\frac{d_1\cdot d_2}{2}$

Plug in the given area and diagonal length. Solve for the other diagonal.

$60\:cm^2=\frac{2\:cm\cdot d_2}{2}$

$2(60\:cm^2)=2(\frac{2\:cm\cdot d_2}{2})$

$120\:cm^2=2\:cm\cdot d_2$

$\frac{120\:cm}{2\:cm}=\frac{2\:cm\cdot d_2}{2\:cm}$

$d_2 =60\:cm$

Report an Error

Example Question #101 : Quadrilaterals

A rhombus contains diagonals with the length $12 \:cm$ and $6 \:cm$ . Find the area of the rhombus.

Possible Answers:

$96\:cm^2$

$88\:cm^2$

$36\:cm^2$

$72\:cm^2$

$54\:cm^2$

Correct answer:

$36\:cm^2$

Explanation:

The equation for the area of a rhombus is given by:

$A= \frac{p \cdot q}{2}$

where and are the two diagonal lengths.

This problem very quickly becomes one of the "plug and chug" type, where the given values just need to be substituted into the equation and the equation then solved. By plugging in the values given, we get:

$A = \frac{12\:cm \cdot 6\:cm}{2}$

$A = \frac{72\:cm^2}2{}$

$A= 36\:cm^2$

Report an Error

Example Question #15 : Rhombuses

Find the area of a rhombus if the diagonals lengths are $20\:cm$ and $40\:cm$ .

Possible Answers:

$800\:cm^2$

$400\:cm^2$

$900\:cm^2$

$600\:cm^2$

$200\:cm^2$

Correct answer:

$400\:cm^2$

Explanation:

Write the formula for the area of a rhombus:

$A=\frac{d_1 \cdot d_2}{2}$

Substitute the given lengths of the diagonals and solve:

$A=\frac{d1 \cdot d2}{2} = \frac{20\:cm \cdot 40\:cm}{2} =\frac{800\:cm^2}{2} = 400\:cm^2$

Report an Error

Example Question #1 : How To Find The Area Of A Rhombus

Find the area of a rhombus if the diagonals lengths are and 5a^2 .

Possible Answers:

10a^3

2a+5a^2

7a^3

5a^2

5a^3

Correct answer:

5a^3

Explanation:

Write the formula for finding the area of a rhombus. Substitute the diagonals and evaluate.

$A=\frac{d1\cdot d2}{2}= \frac{2a \cdot 5a^2}{2}= 5a^3$

Report an Error

Example Question #451 : Plane Geometry

If a side length of a rhombus is half, what is the perimeter of the rhombus?

Possible Answers:

$\frac{\sqrt2}{2}$

$\frac{1}{8}$

Correct answer:

Explanation:

Write the formula to find the perimeter of a rhombus.

P=4s

Substitute the side length and simplify.

$P=4(\frac{1}{2})=2$

Report an Error

Example Question #452 : Plane Geometry

Find the perimeter of a rhombus if the side length is .

Possible Answers:

Correct answer:

Explanation:

Write the formula to find the perimeter of a rhombus.

P=4s

Substitute the side length and solve.

P=4(9)=36

Report an Error

Example Question #3 : How To Find The Perimeter Of A Rhombus

If the side length of a rhombus is $\frac{11}{8}a+\frac{1}{2}b$ , what is the perimeter?

Possible Answers:

$\frac{11}{2}a+2b$

$\frac{11}{8}a^4+\frac{1}{2}b^4$

$\frac{11}{8}a^2+\frac{1}{2}b^2$

4a+4b

$\frac{32}{11}a+\frac{1}{8}b$

Correct answer:

$\frac{11}{2}a+2b$

Explanation:

Write the formula for the perimeter of a rhombus.

P=4s

Substitute the side length and solve for the perimeter.

$P=4\left(\frac{11}{8}a+\frac{1}{2}b\right) = \frac{11}{2}a+2b$

Report an Error

← Previous 1 2 3 4 Next →

View ACT Math Tutors

Germaine
Certified Tutor

Princeton University, Bachelor in Arts, Philosophy.

View ACT Math Tutors

Sakshi
Certified Tutor

M S Ramaiah College of Arts, Science and commerce, Bachelor, Chemistry, Biotechnology, Microbiology .

View ACT Math Tutors

Dr. Charles
Certified Tutor

University of North Alabama, Bachelor of Science, Chemistry. Vanderbilt University, Doctor of Philosophy, Organic Chemistry.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in New York City, GMAT Courses & Classes in Houston, GMAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Phoenix, SAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Denver, GRE Courses & Classes in Washington DC, GRE Courses & Classes in Los Angeles, SSAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Houston, LSAT Test Prep in Denver, MCAT Test Prep in Phoenix, LSAT Test Prep in Houston, GRE Test Prep in Denver, GRE Test Prep in Boston, LSAT Test Prep in Phoenix, ISEE Test Prep in Phoenix, LSAT Test Prep in Washington DC, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Rhombuses

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #11 : How To Find An Angle In A Rhombus

Example Question #12 : How To Find An Angle In A Rhombus

Example Question #13 : How To Find An Angle In A Rhombus

Example Question #15 : How To Find The Length Of The Diagonal Of A Rhombus

Example Question #101 : Quadrilaterals

Example Question #15 : Rhombuses

Example Question #1 : How To Find The Area Of A Rhombus

Example Question #451 : Plane Geometry

Example Question #452 : Plane Geometry

Example Question #3 : How To Find The Perimeter Of A Rhombus

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: