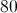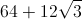We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Parallelograms

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 Next →

Example Question #11 : How To Find An Angle In A Parallelogram

Parallelogram_6

ABCD is a parallelogram. Find y + z .

Possible Answers:

140

100

120

180

Correct answer:

140

Explanation:

In a parallelogram, consecutive angles are supplementary and opposite angles are congruent. Using these properties, we can write a system of equations. Because we have three variables, we will need three equations.

1. $\measuredangle A + \measuredangle B = 180^{\circ}$

2. $\measuredangle B = \measuredangle D$

3. $\measuredangle C + \measuredangle D = 180^{\circ}$

Start with equation 1.

$z + \left (x + z \right ) = 180$

x + 2z = 180

Now simplify equation 2.

x + z = y + 2x

z = y + x

Finally, simplify equation 3.

$\left ( y + 20\right ) + \left ( y+ 2x\right ) = 180$

2y + 2x + 20 = 180

2y + 2x = 160

y + x = 80

Note that we can plug this simplified equation 3 directly into the simplified equation 2 to solve for .

z = y + x = 80

Now that we have , we can solve for using equation 1.

x + 2z = 180

$x + 2\left ( 80\right ) = 180$

x + 160 = 180

x = 20

With , we can solve for using equation 3.

y + x = 80

y + 20 = 80

y = 60

Now that we have and , we can solve for y + z .

y + z = 60 + 80 = 140

Report an Error

Example Question #12 : How To Find An Angle In A Parallelogram

Parallelogram_8

ABCD is a parallelogram. Find .

Possible Answers:

123

171

114

100

Correct answer:

123

Explanation:

In a parallelogram, consecutive angles are supplementary and opposite angles are congruent.

$\measuredangle A + \measuredangle D = 180^{\circ}$

$z + \left ( 2z + 9\right ) = 180$

3z + 9 = 180

3z = 171

z = 57

$\measuredangle A + \measuredangle B = 180^{\circ}$

z + x = 180

57 + x = 180

x = 123

Report an Error

Example Question #1 : Parallelograms

In the parallellogram, what is the value of ?

Screen_shot_2013-07-15_at_9.42.14_pm

Possible Answers:

$130^{\circ}$

$145^{\circ}$

$110^{\circ}$

$120^{\circ}$

$135^{\circ}$

Correct answer:

$130^{\circ}$

Explanation:

Opposite angles are equal, and adjacent angles must sum to 180.

Therefore, we can set up an equation to solve for z:

(z – 15) + 2z = 180

3z - 15 = 180

3z = 195

z = 65

Now solve for x:

2z = x = 130°

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Parallelogram_2

In parallelogram ABCD , $\overline{AB} = 10$ and $\measuredangle A = 60^{\circ}$ . Find $\overline{CD}$ .

Possible Answers:

$8\sqrt{3}$

There is insufficient information to solve the problem.

Correct answer:

Explanation:

In a parallelogram, opposite sides are congruent. Thus,

$\overline{AB} = \overline{CD}$

$10 = \overline{CD}$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Parallelogram_2

In parallelogram ABCD , $\overline{BC} = 30$ and $\measuredangle B = 120^{\circ}$ . Find $\overline{AD}$ .

Possible Answers:

There is insufficient information to solve the problem.

Correct answer:

Explanation:

In a parallelogram, opposite sides are congruent.

$\overline{BC} = \overline{AD}$

$30 = \overline{AD}$

Report an Error

Example Question #3 : How To Find The Length Of The Side Of A Parallelogram

Parallelogram_9

Parallelogram ABCD has an area of 375 . If h = 15 , find $\overline{BC}$ .

Possible Answers:

12.5

There is insufficient information to solve the problem.

Correct answer:

Explanation:

The area of a parallelogram is given by:

A = bh

In this problem, the height is given as and the area is 375 . Both $\overline{AD}$ and $\overline{BC}$ are bases.

$375 = \left ( 15\right )\left ( \overline{BC} \right )$

$\overline{BC} = 25$

Report an Error

Example Question #81 : Quadrilaterals

Parallelogram_10

ABCD is a parallelogram. Find $\overline{AB}$ .

Possible Answers:

There is insufficient information to solve the problem.

17.8

21.5

10.7

23.9

Correct answer:

23.9

Explanation:

$\overline{AB}$ is the hypotenuse of the right triangle formed when we draw the height of the parallelogram. Because it is a right triangle, we can use SOH CAH TOA to solve for $\overline{AB}$ . With respect to $\measuredangle A$ , we know the opposite side of the triangle and we are looking for the hypotenuse. Thus, we can use the sine function to solve for $\overline{AB}$ .

$\sin \left ( \theta\right ) = \frac{\textup{opposite}}{\textup{hypotenuse}}$

$\sin\left ( 42^{\circ}\right ) = \frac{16}{\overline{AB}}$

$\overline{AB} = \frac{16}{\sin\left ( 42^{\circ}\right )}$

$\overline{AB} = 23.9$

Report an Error

Example Question #5 : How To Find The Length Of The Side Of A Parallelogram

Find the length of the base of a parallelogram with a height of and an area of 204 .

Possible Answers:

144

Correct answer:

Explanation:

The formula for the area of a parallelogram is:

A = bh

By plugging in the given values, we get:

$204 = b\cdot12$

b = 17

Report an Error

Example Question #6 : How To Find The Length Of The Side Of A Parallelogram

Parallelogram_11

ABCD is a parallelogram with an area of 510 . Find $\overline{AB}$ .

Possible Answers:

There is insufficient information to solve the problem.

Correct answer:

Explanation:

In order to find $\overline{AB}$ , we must first find . The formula for the area of a parallelogram is:

A = bh

We are given 510 as the area and as the base.

$510 = 34\cdot h$

h = 15

Now, we can use trigonometry to solve for $\overline{AB}$ . With respect to $\measuredangle A$ , we know the opposite side of the right triangle and we are looking for the hypotenuse. Thus, we can use the sine function.

$\sin\left ( \theta\right ) = \frac{\textup{opposite}}{\textup{hypotenuse}}$

$\sin\left ( 62^{\circ}\right ) = \frac{15}{\overline{AB}}$

$\overline{AB} = \frac{15}{\sin \left ( 62^{\circ}\right )} = 17$

Report an Error

Example Question #1 : How To Find The Perimeter Of A Parallelogram

A parallelogram, with dimensions in cm, is shown below. Act1

What is the perimeter of the parallelogram, in cm?

Possible Answers:

$64+12\sqrt{3}$

Correct answer:

$64+12\sqrt{3}$

Explanation:

The triangle on the left side of the figure has a $30^{\circ}$ and a $90^{\circ}$ angle. Since all of the angles of a triangle must add up to $180^{\circ}$ , we can find the angle measure of the third angle:

30+90=120

$180-120=60^{\circ}$

Our third angle is $60^{\circ}$ and we have a 30-60-90 triangle.

A 30-60-90 triangle has sides that are in the corresponding ratio of $x-x\sqrt{3}-2x$ . In this case, the side opposite our $30^{\circ}$ angle is , so

x=6

We also now know that

$x\sqrt{3}=6\sqrt{3}$

2x=12

Now we know all of our missing side lengths. The right and left side of the parallelogram will each be . The bottom and top will each be $20+6\sqrt{3}$ . Let's combine them to find the perimeter:

Perimeter=2w+2l

$2\cdot (12)+2\cdot (20+6\sqrt{3})$

$24+40+12\sqrt{3}$

$64+12\sqrt{3}$

Report an Error

← Previous 1 2 3 4 Next →

View ACT Math Tutors

Njoku
Certified Tutor

Regents College Canterbury University, Bachelor in Arts, Political Science and Government. SUNY at Binghamton, Certificate, F...

View ACT Math Tutors

Rahul
Certified Tutor

University of Calgary , Master's/Graduate, Aerospace engineering .

View ACT Math Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in Boston, Spanish Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in New York City, SSAT Courses & Classes in Chicago, GMAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Atlanta, MCAT Courses & Classes in Philadelphia

Popular Test Prep

ACT Test Prep in Boston, GRE Test Prep in San Diego, ACT Test Prep in New York City, GMAT Test Prep in Miami, GMAT Test Prep in Atlanta, LSAT Test Prep in Chicago, LSAT Test Prep in Atlanta, ACT Test Prep in Chicago, GMAT Test Prep in San Diego, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Parallelograms

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #11 : How To Find An Angle In A Parallelogram

Example Question #12 : How To Find An Angle In A Parallelogram

Example Question #1 : Parallelograms

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Example Question #3 : How To Find The Length Of The Side Of A Parallelogram

Example Question #81 : Quadrilaterals

Example Question #5 : How To Find The Length Of The Side Of A Parallelogram

Example Question #6 : How To Find The Length Of The Side Of A Parallelogram

Example Question #1 : How To Find The Perimeter Of A Parallelogram

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: