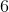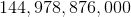ACT Math : Permutation / Combination
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #11 : Permutation / Combination
A university can send 3 track athletes and 2 field athletes to an upcoming sports event. The university has 14 track athletes and 10 field athletes who qualify. How many different teams can be chosen to attend the sports event?
840
140
64,800
16,380
10,080
16,380
The number of different teams that could be chosen is C(14, 3) × C(10, 2) = 16,380.
Example Question #11 : How To Find The Greatest Or Least Number Of Combinations
The menu above is from Lena’s Italian Kitchen. If you are going there for dinner, how many different combinations of a meal and a salad are there?
15
10
5
25
20
20
Combinations = # first option * # second option
= # meals * # salads
= 5 * 4 = 20
Example Question #11 : Permutation / Combination
A student is taking a test consisting of six questions. It is a multiple choice test and each question has four answers labelled A, B, C, and D. How many ways can the student answer all six questions if he does not choose the same answer for any two consecutive questions?
30
625
324
972
100
972
the student has four choices for the first question, but only three choices for each of the remaining questions since he does not choose answers with the same letter twice in a row. From the multiplicative counting principle, there are 4 × 3 × 3 × 3 × 3 x 3 = 972 ways Steve can answer the six questions.
Example Question #11 : Permutation / Combination
Ashley is modeling a new mix-and-match clothing line. Her stylist has selected 5 tops, 3 skirts, and 4 jackets for her photo shoot. Assuming that an outfit consists of one top, one skirt, and one jacket, how many outfits can Ashley create for the photo shoot?
20
12
45
30
60
60
In order to calculate the total possible number of combinations, we must multiply the number of possibilities for each piece by one another.
Example Question #11 : Permutation / Combination
In how many ways can the seven members of a students’ council pose in a line for a yearbook photograph if the chair and vice-chair must be side by side?
First find the number of arrangements in which the chair and vice-chair are together. Consider the chair and vice-chair as a unit. This pair as one unit can be arranged with the remaining five members in 
Therefore, there is a total of 2 * 720 = 1440 ways in which the chair and vice-chair are together.
Example Question #12 : Permutation / Combination
Sally is putting on jewelry and has decided to wear one necklace, one pair of earrings, and one ring. Her jewelry collection is listed below. How many different combinations of jewelry can she wear?
|
Necklace |
Earrings |
Ring |
|
short |
studs |
gold |
|
long |
hoops |
silver |
|
|
dangling |
|
18
3
36
12
7
12
To find the number of different combinations, we must use the fundamental counting principal to multiply the number of options in each category together:
(2)(3)(2) = 12
Example Question #1 : How To Find Permutation Notation
In permutation notation, what does 8P4 represent?
336
1680
6720
210
1680
The expression 8P4 represents the number of permutations of 8 objects arranged 4 at a time. Thus, 8 x 7 x 6 x 5 = 1680
Example Question #11 : Permutation / Combination
How many different ways can five books be lined up on a shelf?
80
150
100
60
120
120
Order matters, so we use permutations: (5)(4)(3)(2)(1) = 120
There are five possibilities for the first book, four possibilities for the second book, three for the third, and two for the fourth, and one possibility for the last book.
Example Question #1721 : Act Math
How many different ways can cheese slices be stacked in piles containing 
Since the order matters, you are dealing with a permutation in this question. A permutation like this could be done with the equation:
For our values, this would be:
However, it is easiest just to think of this like it has 
more easily.
This is 
Certified Tutor
All ACT Math Resources
