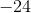ACT Math : Negative Numbers
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1602 : Act Math
What is 1 + (–1) – (–3) + 4 ?
6
9
1
3
7
7
You simplify the expression to be 1 – 1 + 3 + 4 = 7
Example Question #1 : Negative Numbers
Solve the following equation for 
To begin, we need to recall how to subtract negative numbers. Remember, when subtracting a negative number, the two negatives cancel out, creating a positive.
So, this:
Becomes this:
We can combine like terms on the left to get:
Then, we can subtract 
In this case, we are subtracting from a negative number, which is just like adding two negative numbers, or subtracting from a positive number. The result will be more negative, because we will be moving further to the left on the number line.
Example Question #1 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
Compute the following:
Convert all the double signs to a single sign before solving. Remember, two minus (negative) signs combine to form a plus (positive) sign, and a plus (positive) sign and a minus (negative) sign combine to form a minus (negative) sign.
Example Question #1 : How To Multiply Negative Numbers
If a = –2 and b = –3, then evaluate a3 + b2
1
9
5
8
17
1
When multiplying negative numbers, we get a negative answer if there are an odd number of negative numbers being multiplied. We get a positive answer if there are an even number of negative numbers being multiplied.
a3 + b2 becomes (–2)3 + (–3)2 which equals –8 + 9 = 1
Example Question #1 : How To Multiply Negative Numbers
Evaluate:
–3 * –7
10
21
–10
–21
4
21
Multiplying a negative number and another negative number makes the product positive.
Example Question #11 : Arithmetic
Evaluate.
Multiplying a negative and a positive number creates a negative product:
Example Question #5 : Negative Numbers
Solve.
A negative number multiplied by a positive number will always be negative.
Example Question #2 : How To Multiply Negative Numbers
Evaluate 3x3 + x2 if x = –2
–20
28
–22
14
–20
When multiplying a negative number an odd number of times, the answer is negative. When multiplying a negative number an even number of times, the answer is positive. Order of operations also applies: Parentheses, Exponents, Multiplication and Division, Addition and Subtraction, from left to right. A mnemonic to remember the order of operations is “Please excuse my dear Aunt Sally.”
3(–2)3 + (–2)2
= 3(–8) + (4)
= –24 + 4
= –20
Example Question #2 : How To Multiply Negative Numbers
Simplify the following expression: (–4)(2)(–1)(–3)
–24
–16
24
12
–24
First, we multiply –4 and 2. A negative and a positive number multiplied together give us a negative number, so (–4)(2) = –8. A negative times a negative is a positive so (–8)(–1) = 8. (8)(–3) = –24.
Example Question #1 : How To Multiply Negative Numbers
Evaluate the following:
Two odd numbers multiplied always result in an even number. Simply multiple the two as though they were even. Thus
All ACT Math Resources
