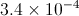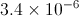Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : How to use scientific notation

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Use Scientific Notation

What is the sum of the solutions of the equation x²-2x-8=0?

Possible Answers:

-2

-10

-6

Correct answer:

Explanation:

The equation factors to (x-4)(x+2)=0, indicating that the roots are x=-2,4. The sum of these two roots is 2.

Report an Error

Example Question #1 : How To Use Scientific Notation

What is the number 350,000,000 in scientific notation?

Possible Answers:

3.5 x 10⁷

3.5 x 10⁵

3.5 x 10⁶

3.5 x 10⁹

3.5 x 10⁸

Correct answer:

3.5 x 10⁸

Explanation:

350,000,000 = 3.5 x 10⁸(exponent is equal to the number of decimal points shifted)

Report an Error

Example Question #2 : How To Use Scientific Notation

Given the equation 2xy + 4x² - y = 2x, if x = 2, what does y equal?

Possible Answers:

-4

Correct answer:

-4

Explanation:

We plug in the value given for x and solve for y.

2xy + 4x² - y = 2x

2(2)y + 4(2)² - y = 2(2)

4y + 4(4) - y = 4

4y - y + 16 = 4

3y = -12

y = -4

Report an Error

Example Question #1 : Other Exponents

How do you express 657,800 in scientific notation?

Possible Answers:

65.78 × 10⁴

6.578 × 10³

65.78 × 10³

6.578 × 10⁴

65.78 × 10⁶

Correct answer:

65.78 × 10⁴

Explanation:

657800 = 6.578 × 10⁵

657800 = 65.78 × 10⁴

Exponent on 10 is the number of decimal points over the number has shifted.

Report an Error

Example Question #2 : How To Use Scientific Notation

2 × 10⁰ + 3 × 10² + 4 × 10⁴ = ?

Possible Answers:

4,032

40,320

400,032

432

40,302

Correct answer:

40,302

Explanation:

2 × 10⁰ + 3 × 10² + 4 × 10⁴ =

2 + 300 + 40,000 = 40,302

Report an Error

Example Question #1 : Other Exponents

Give this number in scientific notation:

$\displaystyle 125,000,000$

Possible Answers:

$12.5\times 10^{10}$ $\displaystyle 12.5\times 10^{10}$

$1.25\times 10^{9}$ $\displaystyle 1.25\times 10^{9}$

$12.5\times 10^{8}$ $\displaystyle 12.5\times 10^{8}$

$1.25\times 10^{7}$ $\displaystyle 1.25\times 10^{7}$

$1.25\times 10^{8}$ $\displaystyle 1.25\times 10^{8}$

Correct answer:

$1.25\times 10^{8}$ $\displaystyle 1.25\times 10^{8}$

Explanation:

There are six zeros and two more number places, for a total of eight, so 125,000,000 is equivalent to $1.25 \times 10^{8}$ $\displaystyle 1.25 \times 10^{8}$ .

Report an Error

Example Question #2 : Other Exponents

Simplify the following expression:

$(4(i^{2}-3))^{\frac{1}{2}}$ $\displaystyle (4(i^{2}-3))^{\frac{1}{2}}$

Possible Answers:

$\displaystyle 16$

$\displaystyle 4i$

$\displaystyle -4$

$\displaystyle 2i$

Correct answer:

$\displaystyle 4i$

Explanation:

$(4(i^{2}-3))^{\frac{1}{2}} =(4(-1-3))^{\frac{1}{2}} =(4(-4))^{\frac{1}{2}}$ $\displaystyle (4(i^{2}-3))^{\frac{1}{2}} =(4(-1-3))^{\frac{1}{2}} =(4(-4))^{\frac{1}{2}}$

$=(-16))^{\frac{1}{2}}=\sqrt{-16}=\sqrt{(16)(-1)}=4i$ $\displaystyle =(-16))^{\frac{1}{2}}=\sqrt{-16}=\sqrt{(16)(-1)}=4i$

Report an Error

Example Question #1 : How To Use Scientific Notation

What is the number $\dpi{100} \small 256,000,000,000$ in scientific notation?

Possible Answers:

$\dpi{100} \small 2.56\times 10^{11}$

$\dpi{100} \small 2.56\times 10^{13}$

$\dpi{100} \small 2.56\times 10^{10}$

$\dpi{100} \small 2.56\times 10^{12}$

$\dpi{100} \small 2.56\times 10^{9}$

Correct answer:

$\dpi{100} \small 2.56\times 10^{11}$

Explanation:

$\dpi{100} \small 256,000,000,000 = 2.56\times 10^{11}$

The exponent is equal to the number of decimal points shifted.

Report an Error

Example Question #2 : How To Use Scientific Notation

Convert from scientific to decimal notation:

$2.3\times 10^{4}$ $\displaystyle 2.3\times 10^{4}$

Possible Answers:

0.0023 $\displaystyle 0.0023$

0.00023 $\displaystyle 0.00023$

23,000 $\displaystyle 23,000$

230,000 $\displaystyle 230,000$

2300 $\displaystyle 2300$

Correct answer:

23,000 $\displaystyle 23,000$

Explanation:

In this case the exponent is positive hence you have to move the decimal point 4 places to the right from where it is in the problem giving us

23,000 $\displaystyle 23,000$

Report an Error

Example Question #4 : How To Use Scientific Notation

Convert from decimal to scientific notation:

$\displaystyle 0.0000034$

Possible Answers:

$3.4\times 10^{-6}$ $\displaystyle 3.4\times 10^{-6}$

$3.4\times 10^{-5}$ $\displaystyle 3.4\times 10^{-5}$

$3.4\times 10^{7}$ $\displaystyle 3.4\times 10^{7}$

$3.4\times 10^{-4}$ $\displaystyle 3.4\times 10^{-4}$

$3.4\times 10^{6}$ $\displaystyle 3.4\times 10^{6}$

Correct answer:

$3.4\times 10^{-6}$ $\displaystyle 3.4\times 10^{-6}$

Explanation:

In this case you have to move the decimal point 6 places to the right. When you move the decimal point to the right the exponent becomes negative. Similarly when you move the decimal point to the left the exponent is positive. Also, to the left of the decimal place there can be only one digit.

$3.4* 10^{-6}$ $\displaystyle 3.4* 10^{-6}$

Report an Error

View ACT Math Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

View ACT Math Tutors

Austyn
Certified Tutor

Morehead State University, Bachelor of Education, Mathematics Teacher Education. Morehead State University, Master of Arts, M...

View ACT Math Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Atlanta, GMAT Courses & Classes in Boston, Spanish Courses & Classes in Chicago, GRE Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in New York City, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Boston, GMAT Test Prep in Miami, LSAT Test Prep in Atlanta, GRE Test Prep in Miami, GRE Test Prep in Los Angeles, SSAT Test Prep in Philadelphia, ISEE Test Prep in New York City, SAT Test Prep in Chicago, MCAT Test Prep in Seattle, GRE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : How to use scientific notation

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : How To Use Scientific Notation

Example Question #1 : How To Use Scientific Notation

Example Question #2 : How To Use Scientific Notation

Example Question #1 : Other Exponents

Example Question #2 : How To Use Scientific Notation

Example Question #1 : Other Exponents

Example Question #2 : Other Exponents

Example Question #1 : How To Use Scientific Notation

Example Question #2 : How To Use Scientific Notation

Example Question #4 : How To Use Scientific Notation

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: