All ACT Math Resources
Example Questions
Example Question #1 : How To Graph A Function
The Y axis is a _______________ of the function Y = 1/X
Zero solution
Vertical slope
Asymptote
Equation
Asymptote
A line is an asymptote in a graph if the graph of the function nears the line as X or Y gets larger in absolute value.
Example Question #1 : How To Graph A Function
Which of the given functions is depicted below?

The graph has x-intercepts at x = 0 and x = 8. This indicates that 0 and 8 are roots of the function.
The function must take the form y = x(x - 8) in order for these roots to be true.
The parabola opens downward, indicating a negative leading coefficient. Expand the equation to get our answer.
y = -x(x - 8)
y = -x2 + 8x
y = 8x - x2
Therefore, the answer must be y = 8x - x2
Example Question #2 : How To Graph A Function
What is the domain of the following function:
x ≠ 2
x ≠ 5
x ≠ –1
x = all real numbers
x ≠ –2 and x ≠ –3
x ≠ –2 and x ≠ –3
The denominator cannot be zero, otherwise the function is indefinite. Therefore x cannot be –2 or –3.
Example Question #2 : How To Graph A Function
The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?
One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.
Example Question #2 : How To Graph A Function
Below is the graph of the function :
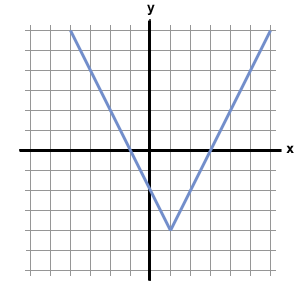
Which of the following could be the equation for ?
First, because the graph consists of pieces that are straight lines, the function must include an absolute value, whose functions usually have a distinctive "V" shape. Thus, we can eliminate f(x) = x2 – 4x + 3 from our choices. Furthermore, functions with x2 terms are curved parabolas, and do not have straight line segments. This means that f(x) = |x2 – 4x| – 3 is not the correct choice.
Next, let's examine f(x) = |2x – 6|. Because this function consists of an abolute value by itself, its graph will not have any negative values. An absolute value by itself will only yield non-negative numbers. Therefore, because the graph dips below the x-axis (which means f(x) has negative values), f(x) = |2x – 6| cannot be the correct answer.
Next, we can analyze f(x) = |x – 1| – 2. Let's allow x to equal 1 and see what value we would obtain from f(1).
f(1) = | 1 – 1 | – 2 = 0 – 2 = –2
However, the graph above shows that f(1) = –4. As a result, f(x) = |x – 1| – 2 cannot be the correct equation for the function.
By process of elimination, the answer must be f(x) = |2x – 2| – 4. We can verify this by plugging in several values of x into this equation. For example f(1) = |2 – 2| – 4 = –4, which corresponds to the point (1, –4) on the graph above. Likewise, if we plug 3 or –1 into the equation f(x) = |2x – 2| – 4, we obtain zero, meaning that the graph should cross the x-axis at 3 and –1. According to the graph above, this is exactly what happens.
The answer is f(x) = |2x – 2| – 4.
Example Question #3 : How To Graph A Function
Which of the following could be a value of for ?
The graph is a down-opening parabola with a maximum of . Therefore, there are no y values greater than this for this function.
Example Question #3 : How To Graph A Function

What is the equation for the line pictured above?
A line has the equation
where is the intercept and is the slope.
The intercept can be found by noting the point where the line and the y-axis cross, in this case, at so .
The slope can be found by selecting two points, for example, the y-intercept and the next point over that crosses an even point, for example, .
Now applying the slope formula,
which yields .
Therefore the equation of the line becomes:
Example Question #3 : Graphing
Which of the following graphs represents the y-intercept of this function?





Graphically, the y-intercept is the point at which the graph touches the y-axis. Algebraically, it is the value of when .
Here, we are given the function . In order to calculate the y-intercept, set equal to zero and solve for .
So the y-intercept is at .
Example Question #133 : Coordinate Geometry
Which of the following graphs represents the x-intercept of this function?





Graphically, the x-intercept is the point at which the graph touches the x-axis. Algebraically, it is the value of for which .
Here, we are given the function . In order to calculate the x-intercept, set equal to zero and solve for .
So the x-intercept is at .
Example Question #134 : Coordinate Geometry
Which of the following represents ?



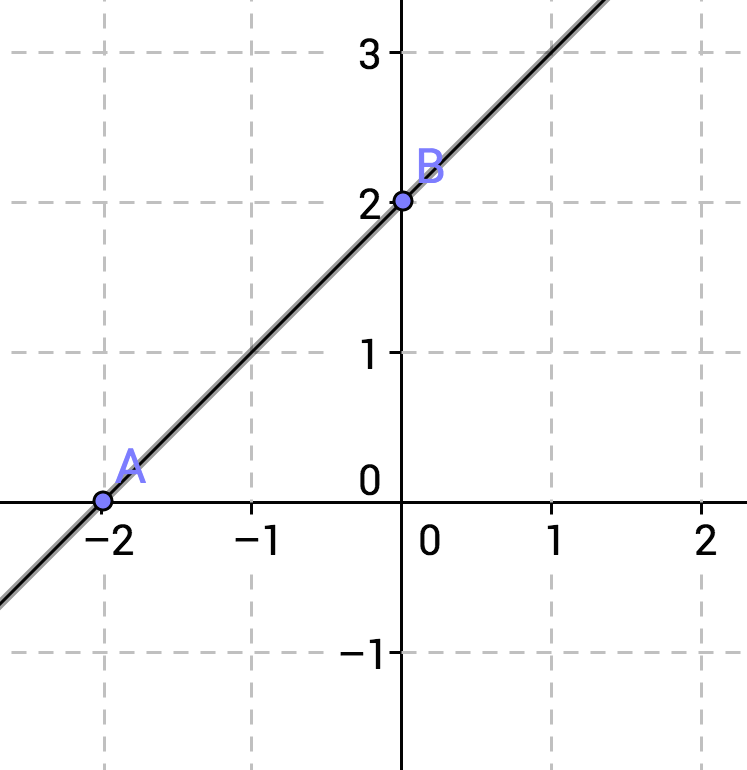

A line is defined by any two points on the line. It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.
Let . Then
So our first set of points (which is also the y-intercept) is
Let . Then
So our second set of points (which is also the x-intercept) is .
Certified Tutor
All ACT Math Resources











































































