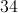ACT Math : How to find the solution to an equation
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #32 : Algebra
How much water should be added to 
Pure water is 0% and pure solution 100%. Let 
So the equation to solve becomes
and
Example Question #31 : Linear / Rational / Variable Equations
Solve 
This problem is a good example of the substitution method of solving a system of equations. We start by rewritting the first equation in terms of 
Solving this equation gives 
Example Question #43 : Linear / Rational / Variable Equations
Joy bought some art supplies. She bought colored pencils for $1.25 per box and sketch pads for $2.25 each. Joy bought one more sketch pad than colored pencil boxes and spent $9.25. How many sketch pads did she buy?
Let 
So the equation to solve becomes 
Solving this equations leads to 2 colored pencil boxes and 3 sketch pads.
Example Question #36 : How To Find The Solution To An Equation
This question deals with absolute value equations which will normally gives you two solutions.
You need to solve two sets of equations for absolute value problems:
and
Example Question #141 : Algebra
Steve sells cars. His monthly salary is $1,000. He gets a $500 commission for each car he sells. If Steve wants to make $7,500 this month, how many cars would he have to sell?
Let 
So
Example Question #1813 : Sat Mathematics
A chemistry student needs to dilute some acid. How much pure water should be added to 2 gallons of 80% acid solution to yield 20% acid solution?
Let pure water = 0 % and pure acid = 100%
The general equation to use is:
So the equation to solve becomes 
Example Question #41 : How To Find The Solution To An Equation
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sell for $75 a piece.
What is the monthly break-even point?
The break-even point is where the costs equal revenue.
Let 
Costs:
Revenue:
So the equation to solve becomes
So the break-even point occurs when they sell 25 widgets.
Example Question #41 : Equations / Inequalities
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sells for $75 a piece.
The Widget Company wants to make a profit of $3,000. How many widgets must be sold?
Profits = Revenues - Costs
Revenue:
Costs:
Profit:
So the equation to solve becomes
So a $3,000 profit occurs when they sell 125 widgets
Example Question #41 : How To Find The Solution To An Equation
Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.
How many picture frames must Sally sell in order to break even?
The break-even point is where the costs equal the revenues.
Let 
Costs:
Revenues:
Thus,
So 14 picture frames must be sold each month to break-even.
Example Question #143 : Algebra
Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.
To make a profit of $500, how many frames need to be sold?
Let 
Revenues:
Costs:
Profits =
So the equation to solve becomes
So 34 picture frames must be sold to make a $500 profit.
All ACT Math Resources
