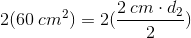All ACT Math Resources
Example Questions
Example Question #11 : How To Find The Length Of The Diagonal Of A Rhombus
If the area of a rhombus is 

Possible Answers:
Correct answer:
Explanation:
Write the formula for the area of a rhombus.
Plug in the given area and diagonal length. Solve for the other diagonal.
Reza
Certified Tutor
Certified Tutor
University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.
All ACT Math Resources
ACT Math Tutors in Top Cities:
Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors
Popular Courses & Classes
ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Houston, GRE Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in Houston, LSAT Courses & Classes in Denver, GRE Courses & Classes in Atlanta