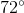ACT Math : How to find an angle in a trapezoid
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : How To Find An Angle In A Trapezoid
Find the measure of angle 
The sum of the angles in any quadrilateral is 360°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360° gives the sum of the two top angles, and dividing the resulting 216° by 2 yields the measurement of x, which is 108°.
Example Question #2 : How To Find An Angle In A Trapezoid
Trapezoid 
As a rule, adjacent (non-paired) angles in a trapezoid are supplementary. Thus, we know that if 
Example Question #1 : How To Find An Angle In A Trapezoid
In the isosceles trapezoid above,
In degrees, what is the measure of 
To find the measure of angle DAC, we must know that the interior angles of all triangles sum up to 180 degrees. Also, as this is an isosceles trapezoid, 
Thus, 
Thus, 
Now that we know two angles out of the three in the triangle on the left, we can subtract them from 180 degrees to find 
Example Question #2 : How To Find An Angle In A Trapezoid
Given the following isosceles triangle:
In degrees, find the measure of the sum of 
All quadrilaterals' interior angles sum to 360°. In isosceles trapezoids, the two top angles are equal to each other.
Similarly, the two bottom angles are equal to each other as well.
Therefore, to find the sum of the two bottom angles, we subtract the measures of the top two angles from 360:
Certified Tutor
All ACT Math Resources
