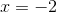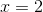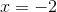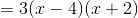Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : How to factor the quadratic equation

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Factor The Quadratic Equation

What are the two solutions to the following quadratic equation?

$3x^{2} - 6x - 24$ $\displaystyle 3x^{2} - 6x - 24$

Possible Answers:

x=-2 $\displaystyle x=-2$ and x=2 $\displaystyle x=2$

x=-2 $\displaystyle x=-2$ and x=-2 $\displaystyle x=-2$

x=-2 $\displaystyle x=-2$ and x=4 $\displaystyle x=4$

x=-4 $\displaystyle x=-4$ and x=2 $\displaystyle x=2$

x=2 $\displaystyle x=2$ and x=2 $\displaystyle x=2$

Correct answer:

x=-2 $\displaystyle x=-2$ and x=4 $\displaystyle x=4$

Explanation:

The equation can be factored.

First pull out a common factor of three from each term.

$\displaystyle 3x^2 -6x-24 = 3(x^2 -2x -8)$ .

Now, find the factors of the constant term that when added together result in the middle term.

$\displaystyle = 3(x-4)(x+2)$

The roots are what values will make the equation equal $\displaystyle 0$ .

Therefore, the answers are x=4 $\displaystyle x=4$ and x=-2. $\displaystyle x=-2.$

Report an Error

View ACT Math Tutors

David
Certified Tutor

The University of Texas at El Paso, Bachelor of Science, Computational Mathematics. Indiana State University, Master of Scien...

View ACT Math Tutors

Cynthia
Certified Tutor

Arizona State University, Bachelors, Psychology. Arizona State University, Master in Public Health, Psychology.

View ACT Math Tutors

Ying
Certified Tutor

Iowa State University, Master of Science, Mathematics.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Houston, LSAT Courses & Classes in Denver, ISEE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta, Spanish Courses & Classes in Philadelphia, LSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Boston, ACT Courses & Classes in Denver, SSAT Courses & Classes in Chicago

Popular Test Prep

LSAT Test Prep in Los Angeles, MCAT Test Prep in New York City, SAT Test Prep in Chicago, GMAT Test Prep in Denver, ISEE Test Prep in Los Angeles, ISEE Test Prep in San Diego, ACT Test Prep in Denver, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in Miami, SSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : How to factor the quadratic equation

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #11 : How To Factor The Quadratic Equation

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: