All ACT Math Resources
Example Questions
Example Question #1 : Integers
Which of the following is a graph for the values of 



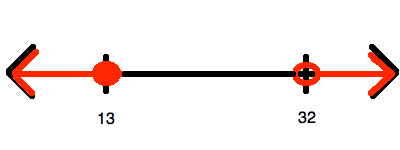


To begin, you must simplify so that you "isolate" 

Now, this inequality represents all of the numbers between 13 and 32. However, it does include 


Example Question #1 : How To Graph An Inequality With A Number Line

Which of the following inequalities is represented by the number line shown above?
Since the inequality represents one range of values between two end points (both of which are included, given the sign being "less than or equal"), you know that whatever you answer, it must be convertible to the form:
Now, you know that it is impossible to get this out of the choices that have no absolute values involved in them. Therefore, the only options that make sense are the two having absolute values; however, here you should choose only the ones that have a 
The wrong answer is simplified in this manner:
And you can stop right here, for you know you will never have 
The other option is simplified in this manner:
This is just what you need!
Example Question #11 : Integers
Which of the following is a graph for the values of 






Begin by solving for 
Now, this is represented by drawing an open circle at 6 and graphing upward to infinity:

Example Question #1631 : Act Math
On a real number line, what is the midpoint of –4 and 18?
4
11
7
8
14
7
The integer halfway between –4 and 18 is 7. The number 7 is 11 greater than –4 and 11 less than 18. Another way to determine this would be to find the average of the two numbers: (–4 + 18)/2 = 14/2 = 7.
Example Question #1 : Number Line
On a number line, what is the distance between –6 and 7?
–1
–13
13
1
3
13
To find distance between two points, take the second and subtract the first.
So 7–(–6) = 7 + 6 = 13
Example Question #1 : Number Line
What is the distance on a number line between 

The distance between 2 numbers on a number line is the sum of their absolute values.
Example Question #1 : Number Line
Which equation can be used to describe the following number line:
![]()
None of the other answers
Solve each equation for 
Example Question #1635 : Act Math
Which number below is farthest from –3 on a number line?
–1
–8
3/2
3
0
3
The answer here relies on knowledge of how numbers are arranged on a number line. We are looking for the number furthest from –3. The number furthest from –3 can lie either to the left of –3 which would be negative numbers that are more negative, or further from 0 than –3. The number furthest from –3 could also lie to its right on the number line, these numbers include all negative numbers between –3 and 0,0, and all positive numbers. The number that satisifes these conditions and is the furthest from –3 on the number line is –8
Example Question #1 : How To Find The Least Common Multiple
What is the least common multiple of 4 and 6?
10
12
24
20
16
12
12 is the least common multiple of 4 and 6.
Example Question #2 : How To Find The Least Common Multiple
What is the least common multiple of 8, 25, and 40?
Find the multiples of 40, and find the smallest one that is divisible by 8 and 25.
All ACT Math Resources




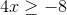




















![[-5] + [12] = 5 + 12 = 17](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/84655/gif.latex)












