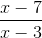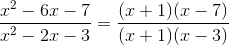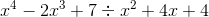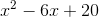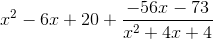ACT Math : Variables
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #3 : How To Add Trinomials
Choose the answer which best simplifies the following expression:
To simplify, remove parentheses and combine like terms:
Example Question #4 : How To Add Trinomials
Choose the answer which best simplifies the following expression:
To simplify, remove parentheses and combine like terms:
Note that adding or subtracting a zero to the end of this equation is unnecessary.
Example Question #5 : How To Add Trinomials
Choose the answer which best simplifies the following expression:
To simplify, simply remove the parentheses and combine like terms:
Example Question #671 : Algebra
A hockey team has 12 forwards, 6 defensemen, and 2 goalies. When they place 3 forwards, 2 defensemen, and 1 goalie on the ice, how many of each type are on the bench, (not on the ice)? F=Forward, D = Defensemen, G= Goalie
4 F, 3 D, 2 G
15 F, 8 D, 3 G
9 F, 4 D, 1 G
6 F, 2 D, 1 G
36 F, 12 D, 2 G
9 F, 4 D, 1 G
We can represent this as a subtraction of trinomials.
(12F + 6D + 2G) – (3F + 2D + 1G) = 9F + 4D + 1G.
Example Question #2162 : Act Math
You go to the grocery store and pick up 
1. Represent the situation with two sets of trinomials:
Before your friends ate the fruit:
The fruit your friends ate:
2. Subtract the first trinomial from the second trinomial:
Example Question #2 : How To Subtract Trinomials
Choose the answer which best simplifies the following expression:
To solve this expression, merely remove the parentheses (bearing in mind that because the second trinomial is being subtracted, it will be negative) and combine like terms:
Example Question #2164 : Act Math
Choose the answer which best simplifies the following expression:
To simplify, remove parentheses and combine like terms:
Example Question #672 : Algebra
Choose the answer which best simplifies the following expression:
To simplify, remove parentheses and combine like terms:
Example Question #1 : How To Divide Trinomials
Simplify the expression:
Once simplified, (x+1) appears on both the numerator and denominator, meaning we can cancel out both of them.
Which gives us:
Example Question #2 : How To Divide Trinomials
Divide:
The set up would look very similar to the division of real numbers, such as when we want to divide 10 by 2 and the answer is 5.
The first step after setting up the "division house" is to see what the first term in the outer trinomial needs to multiplied by to match the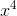 
While we could continue to divide, it would require the use of fraction exponents that would make the answer more complicated. Therefore, the term in red will be the remainder. Because this remainder is still subject to be being divided by the trinomial outside of the division house, we will make the remainder part of the final answer by writing it in fraction form:
Therefore the final answer is
Certified Tutor
Certified Tutor
All ACT Math Resources
