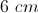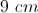All ACT Math Resources
Example Questions
Example Question #16 : Acute / Obtuse Isosceles Triangles
A triangle has a perimeter of 


The answer is 
Since we know that the permieter is 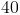


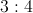





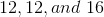

Example Question #231 : Plane Geometry
In the standard 


To form an isosceles triangle here, we need to create a third vertex whose 






Example Question #232 : Plane Geometry

Note: Figure is not drawn to scale.
In the figure above, points 






Because 



We know that 




Example Question #233 : Plane Geometry
A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a 

What is the distance, in feet, between the two sensors?
Round your final answer to the nearest tenth. Do not round until then.
This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of 




Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles 




Plugging in one of our 


Next, cross-multiply:

Now simplify and solve:
Rounding, we see our missing side is 
Example Question #1 : Isosceles Triangles
An isosceles triangle has a base of 


Example Question #234 : Plane Geometry
What is the height of an isosceles triangle which has a base of 

The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
Example Question #1 : How To Find If Of Acute / Obtuse Isosceles Triangles Are Congruent
There are two obtuse triangles. The obtuse angle of triangle one is 

The two triangles cannot be congruent
When the sum of angle A and angle B in triangle 1 is equal to the sum of the corresponding angles in triangle 2
The two triangles must be congruent
When the obtuse angle is congruent to the smallest angle of the other triangle
Cannot be determined
The two triangles cannot be congruent
In order for two obtuse triangles to be congruent, the sum of the two smaller angles must equal the sum of the two smaller angles of the second triangle. That is, excluding the obtuse angle.
The first triangle has an obtuse angle of 




Example Question #1 : How To Find An Angle In A Kite

Using the kite shown above, find the sum of the two remaining congruent interior angles.
The sum of the interior angles of any polygon can be found by applying the formula: 

By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: 


To find the sum of the remaining two angles, determine the difference between 
The solution is:
Thus, 
Check:
Example Question #2 : How To Find An Angle In A Kite
A kite has one set of opposite interior angles where the two angles measure 

Not enough information is provided
The sum of the interior angles of any polygon can be found by applying the formula:


By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: 


The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between 

This means that 

Example Question #3 : How To Find An Angle In A Kite
A kite has one set of opposite interior angles where the two angles measure 

The sum of the interior angles of any polygon can be found by applying the formula: 

A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: 


The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between 

This means that 

All ACT Math Resources