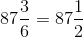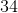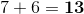Wonderlic : Mathematical functions and reasoning
Study concepts, example questions & explanations for Wonderlic
All Wonderlic Resources
Example Questions
Example Question #11 : Mathematical Functions And Reasoning
A square has perimeter 20 feet. Give its area.
80 square feet
5 square feet
400 square feet
20 square feet
25 square feet
25 square feet
The perimeter of a figure is the sum of the lengths of its sides. A square comprises four sides of equal length, so, if the perimeter of the square is 20 feet, then each side has length
The area of the square is equal to the length of a side multiplied by itself, so the area of this square is
Example Question #12 : Mathematical Functions And Reasoning
Give the arithmetic mean of the following six scores:
83, 87, 99, 90, 82, 84
Round your answer to the nearest whole number.
To find the mean of a group of numbers, add the numbers first:
Divide the sum by the number of scores; this is 6, so
or
This rounds up to 88.
Example Question #1 : Completing Numerical Sequences
10, 15, 22.5, 33.75
What is the next number in the given sequence?
48.78
67.5
50.63
52.54
50.63
The numbers in the given sequence increase in a uniform pattern, namely that half of the previous number is added to each successive number. Half of 33.75 is 16.88, added to 33.75 this gives us the correct answer: 50.63 (which was also the only answer that ended with the appropriate final decimal number.
Example Question #2 : Completing Numerical Sequences
Give the next number in the sequence:
To form the sequence, begin with the term 7. Each subsequent term is equal to 6 added to the previous term, as follows:
the missing term.
Example Question #13 : Mathematical Functions And Reasoning
Which of the following is equal to six hundred seven ten-thousandths?
"Six hundred seven ten-thousandths" is the fraction 
Example Question #14 : Mathematical Functions And Reasoning
Examine the decimal
What is the place value of the position occupied by the "7"?
Hundredths
Ten-thousandths
Tenths
Thousandths
Thousandths
After the decimal point, the place values of the digits are, in order:
The "7" is in the third place after the decimal point, so its place value is one thousandth.
Example Question #15 : Mathematical Functions And Reasoning
The number 0.045 is equal to which of the following?
Forty-five one-hundredths
Forty-five ten-thousandths
Four hundred five ten-thousandths
Four hundred five one-thousandths
Forty-five one-thousandths
Forty-five one-thousandths
After the decimal point, the place values of the digits are, in order:
The last nonzero digit of 0.045 appears in that third place, so the fractional form of this decimal expression is 
Certified Tutor
Certified Tutor
All Wonderlic Resources
