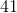All SSAT Upper Level Math Resources
Example Questions
Example Question #502 : Number Concepts And Operations
What number comes next in the sequence?

In order to find the next number in the sequence, take a look at the patterns and common differences between the existing numbers in the sequence. Starting with 




When we get to 




Example Question #503 : Number Concepts And Operations
What is the next number in the sequence?

In order to find the next number in the sequence, take a look at the patterns and common differences between the existing numbers in the sequence. Starting with 




By the time we get to 





Example Question #504 : Number Concepts And Operations
What is the next number in the sequence?

In order to find the next number in the sequence, take a look at the patterns and common differences between the existing numbers in the sequence. Starting at the beginning, we multiply 




We multiply the second 




Example Question #1571 : Ssat Upper Level Quantitative (Math)
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #1572 : Ssat Upper Level Quantitative (Math)
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #1573 : Ssat Upper Level Quantitative (Math)
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #1574 : Ssat Upper Level Quantitative (Math)
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #1575 : Ssat Upper Level Quantitative (Math)
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #11 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
Example Question #12 : How To Find The Common Difference In Sequences
Find the common difference for the arithmetic sequence:
Subtract the first term from the second term to find the common difference.
All SSAT Upper Level Math Resources