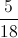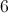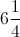Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Number Concepts and Operations

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Complex Fractions

Simplify.

$\frac{x^2+5x+6}{x^2+9x+14}+\frac{x^2+6x+5}{x^2+7x+6}$

Possible Answers:

$\frac{x^2+4x+3}{x^2+13x+42}$

$\frac{x^2+8x+15}{x^2+13x+42}$

$\frac{2x^2+21x+53}{x^2+13x+42}$

$\frac{x^2+3x+2}{x^2+13x+42}$

$\frac{2x^2+8x+15}{x^2+13x+42}$

Correct answer:

$\frac{2x^2+21x+53}{x^2+13x+42}$

Explanation:

Don't try to find the least common denominator as it will take a lot of time and a definite mistake in arithmetic. Instead try to see if these quadratics can simplify.

Upon inspection, we get

$\frac{(x+2)(x+3)}{(x+2)(x+7)}+\frac{(x+1)(x+5)}{(x+1)(x+6)}$ .

Remember, to break down the quadratic equation by finding the binomials, two numbers that are factors of c must add up to make b.

With the cancellations, we should get

$\frac{x+3}{x+7}+\frac{x+5}{x+6}$ .

The common denominator will be (x+6)(x+7), x^2+7x+6x+42 , x^2 + 13x+42.

Remember when foiling, you multiply the numbers/variables that first appear in each binomial, followed by multiplying the outer most numbers/variables, then multiplying the inner most numbers/variables and finally multiplying the last numbers/variables. The left fraction numerator is multiplied by x+6 and the right fraction numerator is multiplied by x+7 .

Overall, the new fraction should read

$\frac{x^2+6x+3x+18+x^2+7x+5x+35}{x^2+13x+42}$ .

After simplification, answer should be $\frac{2x^2+21x+53}{x^2+13x+42}$ .

Report an Error

Example Question #22 : Complex Fractions

Simplify.

$\frac{2x^2+2x-4}{x^2+2x-3}+\frac{x^2-3x-10}{2x^2-8x-10}$

Possible Answers:

$\frac{2x^2+8x+8}{x^2+4x+3}$

None of the above are correct.

$\frac{2x^2+8x+8}{2x^2+8x+6}$

$\frac{5x^2+20x+14}{x^2+4x+3}$

$\frac{5x^2+17x+14}{2x^2+8x+6}$

Correct answer:

$\frac{5x^2+17x+14}{2x^2+8x+6}$

Explanation:

Try to simplify the fraction rather than finding the least common denominator. By breaking the quadratic equation into its factors, it becomes:

$\frac{2(x+2)(x-1)}{(x-1)(x+3)}+\frac{(x-5)(x+2)}{2(x-5)(x+1)}$ .

Remember, to break down the quadratic equation by finding the binomials, two numbers that are factors of c must add up to make b. Also, if the values of a, b, and c in the quadratic equation can be reduced, then factor out that divisor to make the quadratic easier to factor.

Upon cancelling, we should get

$\frac{2(x+2)}{(x+3)}+\frac{(x+2)}{2(x+1)}$ .

The common denominator is $(x+3)\left ( 2x+2\right )$ or (2x^2+2x+6x+6) or 2x^2+8x+6 . Remember when foiling, you multiply the numbers/variables that first appear in each binomial, followed by multiplying the outer most numbers/variables, then multiplying the inner most numbers/variables and finally multiplying the last numbers/variables. Then multiply the numerator of left fraction by 2(x+1) and the numerator of right fraction by (x+3) and the new fraction should look like,

$\frac{4(x^2+x+2x+2)+x^2+2x+3x+6}{2x^2+8x+6}$ .

Upon distributing the four and simplifying the fraction, answer is shown.

$\frac{5x^2+17x+14}{2x^2+8x+6}$

Report an Error

Example Question #23 : Complex Fractions

Simplify.

$\frac{2}{x^2}+\frac{1}{x^3}$

Possible Answers:

$\frac{2x+1}{x^3}$

$\frac{2x+1}{x^4}$

$\frac{3}{x^5}$

$\frac{2x^3+x^2}{x^5}$

Correct answer:

$\frac{2x+1}{x^3}$

Explanation:

Least common denominator is $x^{3}$ . Just multiply the left fraction numerator by and solve.

$\frac{2}{x^2}\cdot \frac{x}{x}+\frac{1}{x^3}=\frac{2x}{x^3}+\frac{1}{x^3}=\frac{2x+1}{x^3}$

Therefore the answer is $\frac{2x+1}{x^3}$ .

Report an Error

Example Question #71 : Fractions

Simplify.

$\frac{x^2-5x}{x^2-25}+\frac{x^2+x-2}{2x^2+3x-2}$

Possible Answers:

$\frac{3x^2+3x-5}{2x^2+9x-5}$

$\frac{2x^2+3x-5}{2x^2+9x-5}$

$\frac{20x^2}{x^2+4x+9}$

$\frac{3x^2+4x-5}{2x^2+9x-5}$

$\frac{x^2+3x-5}{2x^2+9x-5}$

Correct answer:

$\frac{3x^2+3x-5}{2x^2+9x-5}$

Explanation:

Try to simplify the fractions rather than trying to find the least common denominator. It should look like this:

$\frac{x(x-5)}{(x-5)(x+5)}+\frac{(x-1)(x+2)}{(2x-1)(x+2)}$ .

Remember, to break down the quadratic equation by finding the binomials, two numbers that are factors of c must add up to make b. The 2x^2+3x-2 may not be easy to factor but when put into the quadratic formula

$\left(-b\pm \frac{\sqrt{b^2-4ac}}{2a}\right)$ , we get roots of and $\frac{1}{2}$ . Then set equations equal to so that when solving for , the answer is the root.

Now after cancellations, we get $\frac{x}{x+5}+\frac{x-1}{2x-1}$ .

The common denominator is (x+5)(2x-1) or 2x^2-x+10x-5 or 2x^2+9x-5 .

Remember when foiling, you multiply the numbers/variables that first appear in each binomial, followed by multiplying the outer most numbers/variables, then multiplying the inner most numbers/variables and finally multiplying the last numbers/variables. For the left fraction numerator you multiply by what it's lacking and same with the right fraction numerator.

The overall fraction should look like

$\frac{2x^2-x+x^2-x+5x-5}{2x^2+9x-5}$

Once simplified, the answer will be shown.

$\frac{3x^2+3x-5}{2x^2+9x-5}$

Report an Error

Example Question #133 : Number Concepts And Operations

Add: $\frac{\frac{2}{3}}{\frac{1}{8}} + \frac{3}{\frac{8}{3}}$

Possible Answers:

$\frac{97}{12}$

$\frac{40}{3}$

$\frac{29}{24}$

$\frac{155}{24}$

$\frac{131}{24}$

Correct answer:

$\frac{155}{24}$

Explanation:

Rewrite the fractions using a division sign.

$\frac{\frac{2}{3}}{\frac{1}{8}} + \frac{3}{\frac{8}{3}}= \left(\frac{2}{3}\div \frac{1}{8}\right)+\left(3\div \frac{8}{3}\right)$

To change the division sign to a multiplication sign, take the reciprocal of the second terms.

$\left(\frac{2}{3}\div \frac{1}{8}\right)+\left(3\div \frac{8}{3}\right)=\left(\frac{2}{3}\times 8\right)+\left(3\times \frac{3}{8}\right)$

Simplify.

$\left(\frac{2}{3}\times 8\right)+\left(3\times \frac{3}{8}\right)= \frac{16}{3}+\frac{9}{8}$

Find the LCD, and rewrite the fractions to add the numerators.

$\frac{16}{3}+\frac{9}{8} = \frac{128}{24}+ \frac{27}{24}= \frac{155}{24}$

Report an Error

Example Question #1 : How To Find A Complex Fraction

Simplify:

$\frac{\frac{2}{3} + \frac{1}{5}}{\frac{4}{5}}$

Possible Answers:

$\frac{52}{75}$

$\frac{13}{12}$

$\frac{3}{7}$

$\frac{1}{5}$

$\frac{3}{10}$

Correct answer:

$\frac{13}{12}$

Explanation:

Add the fractions in the numerator, then divide the sum by the denominator:

$\frac{\frac{2}{3} + \frac{1}{5}}{\frac{4}{5}}$

$=\frac{\frac{2\cdot 5}{3\cdot 5} + \frac{1\cdot 3}{5\cdot 3}}{\frac{4}{5}}$

$=\frac{\frac{10}{15} + \frac{3}{15}}{\frac{4}{5}}$

$=\frac{\frac{10+3}{15} }{\frac{4}{5}} = \frac{\frac{13}{15} }{\frac{4}{5}}$

$= \frac{13}{15} \div \frac{4}{5} = \frac{13}{15} \times \frac{5}{4} = \frac{13}{3} \times \frac{1}{4} =\frac{13}{12}$

Report an Error

Example Question #2 : How To Find A Complex Fraction

Simplify:

$\frac{\frac{1}{3} + \frac{3}{10}}{\frac{9}{10}}$

Possible Answers:

$\frac{57}{100}$

$\frac{40}{117}$

$\frac{19}{27}$

$\frac{2}{3}$

$\frac{1}{27}$

Correct answer:

$\frac{19}{27}$

Explanation:

Simplify the sum in the numerator, then divide by the denominator:

$\frac{\frac{1}{3} + \frac{3}{10}}{\frac{9}{10}}$

$=\frac{\frac{1\cdot 10}{3 \cdot 10} + \frac{3 \cdot 3}{10 \cdot 3}}{\frac{9}{10}}$

$=\frac{\frac{10}{30} + \frac{9}{30}}{\frac{9}{10}}$

$=\frac{\frac{10+9}{30} }{\frac{9}{10}} = \frac{\frac{19}{30} }{\frac{9}{10}}$

$\frac{19}{30} \div \frac{9}{10} = \frac{19}{30}\times \frac{10}{9} = \frac{19}{3}\times \frac{1}{9} = \frac{19}{27}$

Report an Error

Example Question #131 : Number Concepts And Operations

Simplify:

$\frac{1\frac{1}{3}}{4 \frac{4}{5}}$

Possible Answers:

$\frac{1}{4}$

$\frac{5}{18}$

$\frac{3}{5}$

$\frac{4}{15}$

$\frac{2}{5}$

Correct answer:

$\frac{5}{18}$

Explanation:

Rewrite this as a division problem, then solve:

$\frac{1\frac{1}{3}}{4 \frac{4}{5}} = 1\frac{1}{3} \div 4 \frac{4}{5} = \frac{4}{3} \div \frac{24}{5}= \frac{4}{3} \times \frac{5}{24}= \frac{1}{3} \times \frac{5}{6}= \frac{5}{18}$

Report an Error

Example Question #132 : Number Concepts And Operations

Simplify:

$\frac{5}{1\frac{1}{4}}$

Possible Answers:

$4 \frac{1}{2}$

$6\frac{1}{4}$

$3 \frac{3}{4}$

Correct answer:

Explanation:

Rewrite this as a division problem, then solve:

$\frac{5}{1\frac{1}{4}} = 5 \div 1\frac{1}{4}= \frac{5}{1}\div \frac{5}{4} = \frac{5}{1}\times \frac{4}{5}= \frac{1}{1}\times \frac{4}{1} = 4$

Report an Error

Example Question #4 : How To Find A Complex Fraction

Simplify:

$\frac{3\frac{4}{5}}{3\frac{1}{2}+2\frac{1}{5}}$

Possible Answers:

$\frac{5}{8}$

$\frac{3}{4}$

$\frac{7}{10}$

$\frac{5}{9}$

$\frac{2}{3}$

Correct answer:

$\frac{2}{3}$

Explanation:

$\frac{3\frac{4}{5}}{3\frac{1}{2}+2\frac{1}{5}}$

$=3\frac{4}{5} \div \left ( 3\frac{1}{2}+2\frac{1}{5} \right )$

$= \frac{19}{5} \div \left ( \frac{7}{2}+ \frac{11}{5} \right )$

$=\frac{19}{5} \div \left ( \frac{35}{10}+ \frac{22}{10} \right )$

$=\frac{19}{5} \div \frac{57}{10}$

$=\frac{19}{5} \times \frac{10}{57}$

$=\frac{1 }{1} \times \frac{2}{3} = \frac{2}{3}$

Report an Error

View SSAT- Upper Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Darron
Certified Tutor

Georgia State University, Bachelors, English Education . Liberty University, Masters, Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Washington DC, GRE Tutors in Atlanta, Computer Science Tutors in Atlanta, Statistics Tutors in Chicago, ACT Tutors in Miami, SSAT Tutors in San Francisco-Bay Area, SSAT Tutors in Phoenix, Chemistry Tutors in Los Angeles, Biology Tutors in Chicago, Physics Tutors in Chicago

Popular Courses & Classes

SSAT Courses & Classes in Boston, ISEE Courses & Classes in Phoenix, Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Phoenix, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Miami, MCAT Courses & Classes in New York City, Spanish Courses & Classes in San Diego, GRE Courses & Classes in Washington DC

Popular Test Prep

ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Seattle, GMAT Test Prep in Atlanta, LSAT Test Prep in Philadelphia, MCAT Test Prep in Washington DC, GRE Test Prep in Seattle, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Seattle, SSAT Test Prep in Boston, GRE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Number Concepts and Operations

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #21 : Complex Fractions

Example Question #22 : Complex Fractions

Example Question #23 : Complex Fractions

Example Question #71 : Fractions

Example Question #133 : Number Concepts And Operations

Example Question #1 : How To Find A Complex Fraction

Example Question #2 : How To Find A Complex Fraction

Example Question #131 : Number Concepts And Operations

Example Question #132 : Number Concepts And Operations

Example Question #4 : How To Find A Complex Fraction

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: