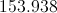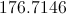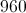We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find the area of a circle

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Area And Circumference Of A Circle

Give the area of a circle that circumscribes a right triangle with legs of length and .

Possible Answers:

$\frac{169 \pi}{2}$

$\frac{676\pi}{3}$

$\frac{169 \pi}{3}$

$169 \pi$

$338 \pi$

Correct answer:

$169 \pi$

Explanation:

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of triangle a diameter.

The length of the hypotenuse of this triangle can be calculated using the Pythagorean Theorem:

$d = \sqrt {10^{2}+24^{2}} = \sqrt{100+576} = \sqrt{676} = 26$

The radius is half this, or 13, so the area is

$A = \pi r^{2} = \pi \cdot 13 ^{2} = 169 \pi$

Report an Error

Example Question #11 : Area And Circumference Of A Circle

A $120 ^{\circ }$ central angle of a circle has a chord with length . Give the area of the circle.

Possible Answers:

$\frac{225 \pi}{4}$

$75 \pi$

$225 \pi$

$\frac{225 \pi}{2}$

$\frac{75 \pi}{2}$

Correct answer:

$75 \pi$

Explanation:

The figure below shows $\angle AOB$ , which matches this description, along with its chord $\overline{AB}$ and triangle bisector $\overline{OM}$ .

Chord

We will concentrate on $\Delta AOM$ , which is a 30-60-90 triangle.

Chord $\overline{AB}$ has length 15, so $AM = \frac{1}{2} AB = \frac{1}{2} \cdot 15 = \frac{15}{2}$

By the 30-60-90 Theorem,

$OM = AM \div \sqrt{3}= \frac{15}{2} \div \sqrt{3}= \frac{15}{2\sqrt{3}}$

and

$AO = 2 \cdot OM = 2 \cdot \frac{15}{2\sqrt{3}} = \frac{15}{ \sqrt{3}}$

This is the radius, so the area is

$A = \pi r^{2} = \pi \cdot \left ( \frac{15}{ \sqrt{3}} \right )^{2}= \frac{225}{3} \pi = 75 \pi$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle that has a diameter of inches?

Possible Answers:

960

153.938

706.8583

153.938

176.7146

960

940

Correct answer:

176.7146

Explanation:

The formula for finding the area of a circle is $\pi r^{2}$ . In this formula, represents the radius of the circle. Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius. In order to do this, we divide the diameter by .

$\frac{15}{2}=7.5$

Now we use 7.5 for in our equation.

$\pi (7.5)^{2}=176.7146 \: in^{2}$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle with a diameter equal to 6?

Possible Answers:

$3\pi$

$9\pi$

$18\pi$

$36\pi$

Correct answer:

$9\pi$

Explanation:

First, solve for radius:

$r=\frac{d}{2}=\frac{6}{2}=3$

Then, solve for area:

$A=r^2\pi=3^2\pi=9\pi$

Report an Error

Example Question #11 : How To Find The Area Of A Circle

The diameter of a circle is $4\ cm$ . Give the area of the circle.

Possible Answers:

$12.56\ cm^2$

$12 \ cm^2$

$13.56\ cm^2$

$11.56\ cm^2$

$13\ cm^2$

Correct answer:

$12.56\ cm^2$

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle, and $\pi$ is approximately 3.14 .

$Area=\frac{\pi d^2}{4}=\frac{\pi\times 4^2}{4}=4\pi \Rightarrow Area\approx 4\times 3.14\Rightarrow Area\approx 12.56 \ cm^2$

Report an Error

Example Question #2 : Area Of A Circle

The diameter of a circle is . Give the area of the circle in terms of .

Possible Answers:

11.56 t^2

12.56 t

12.56 t^2

12 t^2

11.56 t

Correct answer:

12.56 t^2

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle and $\pi$ is approximately 3.14 .

$Area=\frac{\pi (4t)^2}{4}=\frac{16\pi t^2}{4}=4\pi t^2 \Rightarrow Area\approx 4\times 3.14\times t^2$

$\Rightarrow Area\approx 12.56t^2$

Report an Error

Example Question #3 : How To Find The Area Of A Circle

The radius of a circle is $\frac{2}{\sqrt{\pi }}$ . Give the area of the circle.

Possible Answers:

$4\pi$

$2\pi$

$\frac{4}{\pi }$

Correct answer:

Explanation:

The area of a circle can be calculated as $Area=\pi r^2$ , where is the radius of the circle, and $\pi$ is approximately 3.14 .

$Area=\pi r^2=\pi\times (\frac{2}{\sqrt{\pi}})^2=\pi\times \frac{4}{\pi}\Rightarrow Area=4$

Report an Error

Example Question #3 : How To Find The Area Of A Circle

The perpendicular distance from the chord to the center of a circle is $\sqrt{2}t$ , and the chord length is $2\sqrt{2}t$ . Give the area of the circle in terms of .

Possible Answers:

11.56t^2

12.56t

11.56t

12t

12.56t^2

Correct answer:

12.56t^2

Explanation:

Chord length = $2\sqrt{r^2-d^2}$ , where is the radius of the circle and is the perpendicular distance from the chord to the circle center.

Chord length = $2\sqrt{r^2-d^2}\Rightarrow (2\sqrt{2})t=2\sqrt{r^2-(\sqrt{2}t)^2}$

$\Rightarrow 8t^2=4(r^2-2t^2)\Rightarrow 4r^2=16t^2\Rightarrow r^2=4t^2\Rightarrow r=2t$

$Area=\pi r^2$ , where is the radius of the circle and $\pi$ is approximately 3.14 .

$Area=\pi r^2=3.14\times (2t)^2=12.56t^2$

Report an Error

Example Question #3 : Area Of A Circle

The circumference of a circle is 12.56 inches. Find the area of the circle.

Let $\pi = 3.14$ .

Possible Answers:

$12\ in^2$

$11.56\ in^2$

$12.56\ in^2$

$11\ in^2$

$13.56\ in^2$

Correct answer:

$12.56\ in^2$

Explanation:

First we need to find the radius of the circle. The circumference of a circle is $Circumference =2\pi r$ , where is the radius of the circle.

$12.56=2\times 3.14\times r\Rightarrow r=2\ in$

The area of a circle is $Area=\pi r^2$ where is the radius of the circle.

$Area=\pi r^2=3.14\times 2^2=12.56\ in^2$

Report an Error

Example Question #12 : How To Find The Area Of A Circle

Find the area of a circle with a radius of 100.

Possible Answers:

$2500\pi$

$1000\pi$

$100\textup{,}}000\pi$

$10\textup{,}}000\pi$

$100\pi$

Correct answer:

$10\textup{,}}000\pi$

Explanation:

Write the formula for a circle.

$A=\pi r^2$

Substitute the radius.

$A=\pi r^2= \pi(100)^2= 10000\pi$

Report an Error

View SSAT- Upper Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Upper Level Tutors

Brianna
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. National University of Ireland at Galway, Master of Science, Neu...

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in San Diego, Biology Tutors in Boston, Statistics Tutors in Seattle, GRE Tutors in San Diego, Biology Tutors in Chicago, Algebra Tutors in Miami, SSAT Tutors in Houston, Algebra Tutors in Philadelphia, ACT Tutors in San Francisco-Bay Area, GRE Tutors in Philadelphia

Popular Courses & Classes

Spanish Courses & Classes in Denver, Spanish Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Miami, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Washington DC, GMAT Courses & Classes in New York City, SAT Courses & Classes in Houston, SSAT Courses & Classes in Seattle, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Boston

Popular Test Prep

GMAT Test Prep in Washington DC, ISEE Test Prep in San Diego, GMAT Test Prep in Houston, LSAT Test Prep in Chicago, ACT Test Prep in San Francisco-Bay Area, SSAT Test Prep in New York City, SAT Test Prep in San Diego, SAT Test Prep in Chicago, ISEE Test Prep in Boston, SAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find the area of a circle

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #11 : Area And Circumference Of A Circle

Example Question #11 : Area And Circumference Of A Circle

Example Question #1 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #11 : How To Find The Area Of A Circle

Example Question #2 : Area Of A Circle

Example Question #3 : How To Find The Area Of A Circle

Example Question #3 : How To Find The Area Of A Circle

Example Question #3 : Area Of A Circle

Example Question #12 : How To Find The Area Of A Circle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: