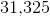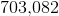Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find consecutive integers

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Sequences And Series

Three consecutive even integers have sum 924. What is the product of the least and greatest of the three?

Possible Answers:

93,632

No three consecutive even integers have sum 924.

96,096

94,860

97,340

Correct answer:

94,860

Explanation:

Let the middle integer of the three be . The three integers are therefore

x-2, x, x+2 , and they can be found using the equation

$\left (x-2 \right )+ x +\left ( x+2 \right ) = 924$

3x= 924

x = 308

The three even integers are therefore 306, 308, and 310, and the product of the least and greatest of these is

$306 \times 310= 94,860$

Report an Error

Example Question #2 : Sequences And Series

Three consecutive odd integers have sum 537. What is the product of the least and greatest of the three?

Possible Answers:

$32\textup{,}037$

$29\textup{,}237$

$30\textup{,}621$

$31\textup{,}325$

$29\textup{,}925$

Correct answer:

$32\textup{,}037$

Explanation:

Let the middle integer of the three be . The three integers are therefore

x-2, x, x+2 , and they can be found using the equation

$\left (x-2 \right )+ x +\left ( x+2 \right ) = 537$

3x= 537

x = 1 79

The three integers are 177, 179, and 181, and the product of the least and greatest is

$177 \times 181 = 32,037$

Report an Error

Example Question #3 : Sequences And Series

Four consecutive integers have sum 3,350. What is the product of the middle two?

Possible Answers:

$703\textup{,}082$

$\textup{No four consecutive integers have a sum of 3,350}$

$701\textup{,}406$

$704\textup{,}760$

$699\textup{,}732$

Correct answer:

$701\textup{,}406$

Explanation:

Call the least of the four integers . The four integers are therefore

x, x+1, x+2, x+3 ,

and they can be found using the equation

$x + \left (x+1 \right )+\left (x+2 \right )+\left ( x+3 \right )= 3,350$

4x+6= 3,350

4x=3,344

$x=3,344 \div 4 = 836$

The integers are 836, 837, 838, 839.

To get the correct response, multiply:

$837 \times 838 = 701,406$

Report an Error

Example Question #1 : How To Find Consecutive Integers

Three consecutive integers have sum 427 . What is their product?

Possible Answers:

$\text{No three consecutive integers have sum } 427.$

3,048,480

2,985,840

2,924,064

2,863,146

Correct answer:

$\text{No three consecutive integers have sum } 427.$

Explanation:

Let the middle integer of the three be . The three integers are therefore

x-1, x, x+1 , and they can be found using the equation

$\left (x-1 \right )+ x +\left ( x+1 \right ) = 427$

3x= 427

$x = 142\frac{1}{3}$

This contradicts the condition that the numbers are integers. Therefore, three integers satisfying the given conditions cannot exist.

Report an Error

Example Question #4 : Sequences And Series

Three consecutive integers have a sum of 312 . What is their product?

Possible Answers:

1,190,910

1,124,760

1,157,520

$\text{No three consecutive integers have sum 312.}$

1,092,624

Correct answer:

1,124,760

Explanation:

Let the middle integer of the three be . The three integers are therefore

x-1, x, x+1 , and they can be found using the equation

$\left (x-1 \right )+ x +\left ( x+1 \right ) = 312$

3x= 312

x = 104

The integers are therefore 103, 104, 105. The correct response is their product, which is

$103 \times 104 \times 105= 1,124,760$

Report an Error

Example Question #6 : How To Find Consecutive Integers

1,3,9,x.81

What is the value of is this sequence?

Possible Answers:

243

Correct answer:

Explanation:

This is a geometric sequence since the pattern of the sequence is through multiplication.

You have to multiple each value by to get the next one.

The value before is so 9*3=27 .

Report an Error

Example Question #5 : Sequences And Series

Which of the following can be the sum of four consecutive positive integers?

Possible Answers:

None of the other answers are correct.

178

213

420

143

Correct answer:

178

Explanation:

Let , N+1 , N+2 , and N+3 be the four consecutive integers. Then their sum would be

N + (N+1) + (N+2) + (N+3) = 4N + 6

In other words, if 6 were to be subtracted from their sum, the difference would be a multiple of 4. Therefore, we subtract 6 from each of the choices and see if any of the resulting differences are multiples of 4.

$178 -6 = 172 ; 172 \div4 = 43$

$213 -6 = 207 ; 207 \div4 = 51 \; R \; 3$

$420 -6 = 414 ; 414 \div4 = 103 \: R \: 2$

$143 -6 = 137 ; 137 \div4 = 34\: R\: 1$

Since this only happens in the case of 178, this is the only number of the four that can be a sum of four consecutive integers: 43, 44, 45, 46.

Report an Error

View SSAT- Upper Level Tutors

Donna
Certified Tutor

Indiana University of Pennsylvania-Main Campus, Bachelor of Science, Education of Developmentally Delayed Individuals. Grand ...

View SSAT- Upper Level Tutors

Darian
Certified Tutor

University of North Texas, Current Undergrad Student, English.

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

CUNY College of Staten Island, Bachelor in Arts, Applied Psychology. New York University, Master of Arts, Applied Psychology.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Washington DC, LSAT Tutors in Washington DC, Reading Tutors in San Diego, ACT Tutors in Boston, Calculus Tutors in Houston, Statistics Tutors in Houston, Calculus Tutors in New York City, Reading Tutors in Los Angeles, Biology Tutors in San Diego, Biology Tutors in Denver

Popular Courses & Classes

Spanish Courses & Classes in Chicago, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Phoenix, Spanish Courses & Classes in Seattle, ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Washington DC

Popular Test Prep

LSAT Test Prep in Houston, MCAT Test Prep in Boston, LSAT Test Prep in Chicago, MCAT Test Prep in Chicago, SSAT Test Prep in Seattle, MCAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Atlanta, ACT Test Prep in Seattle, SAT Test Prep in Denver, GRE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find consecutive integers

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : Sequences And Series

Example Question #2 : Sequences And Series

Example Question #3 : Sequences And Series

Example Question #1 : How To Find Consecutive Integers

Example Question #4 : Sequences And Series

Example Question #6 : How To Find Consecutive Integers

Example Question #5 : Sequences And Series

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: