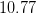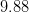Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Coordinate Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Given a line defined by the equation $y=\frac{9}{8}x+4$ , which of the following lines is perpendicular to ?

Possible Answers:

$y=-\frac{8}{9}x+4$

$y=\frac{9}{8}x+4$

$y=-\frac{9}{8}x+4$

$y=\frac{9}{8}x-4$

$y=4x+\frac{9}{8}$

Correct answer:

$y=-\frac{8}{9}x+4$

Explanation:

For a given line defined by the equation y=mx+b , any line perpendicular to must have a slope that is the negative reciprocal of 's slope , $-\frac{1}{m}$ .

In this instance, the slope of line is $m=\frac{9}{8}$ , so $-\frac{1}{m}=-\frac{1}{\frac{9}{8}}=-\frac{8}{9}$ . The only line provided with an equation that has this slope is $y=-\frac{8}{9}x+4$ .

Report an Error

Example Question #2 : How To Find The Equation Of A Perpendicular Line

A given line is defined by the equation $y=\frac{5}{6}x-9$ . What is the slope of any line that is perpendicular to ?

Possible Answers:

Not enough information provided

$\frac{1}{9}$

$-\frac{6}{5}$

$-\frac{5}{6}$

Correct answer:

$-\frac{6}{5}$

Explanation:

For a given line defined by the equation y=mx+b , any line perpendicular to must have a slope that is the negative reciprocal of 's slope , $-\frac{1}{m}$ .

Since in this case $m=\frac{5}{6}$ ,

$-\frac{1}{m}=-\frac{1}{\frac{5}{6}}=\frac{6}{5}$ .

Report an Error

Example Question #441 : Geometry

Which of the following equations represents a line that goes through the point (-2, 6) and is perpendicular to the line 3x + 6y = 12 ?

Possible Answers:

y = 2x + 2

y = 2x + 10

y = 2x + 6

y = -2x + 10

y = -2x + 2

Correct answer:

y = 2x + 10

Explanation:

In order to solve this problem, we need first to transform the equation from standard form to slope-intercept form:

y = mx + b

Transform the original equation to find its slope.

3x + 6y = 12

First, subtract from both sides of the equation.

3x-3x + 6y = 12-3x

Simplify and rearrange.

6y = -3x + 12

Next, divide both sides of the equation by 6.

$\frac{6y}{6} = -\frac{3x}{6} + \frac{12}{6}$

$y = -\frac{1}{2}x+ 2$

The slope of our first line is equal to $-\frac{1}{2}$ . Perpendicular lines have slopes that are opposite reciprocals of each other; therefore, if the slope of one is x, then the slope of the other is equal to the following:

$-\frac{1}{x}$

Let's calculate the opposite reciprocal of our slope:

$-\frac{1}{2}\rightarrow -\left (-\frac{2}{1} \right )=2$

The slope of our line is equal to 2. We now have the following partial equation:

y = 2x + b

We are missing the y-intercept, . Substitute the x- and y-values in the given point (-2, 6) to solve for the missing y-intercept.

6 = 2(-2) + b

6 = -4 + b

Add 4 to both sides of the equation.

6+4 = -4+4 + b

10 = b

Substitute this value into our partial equation to construct the equation of our line:

y = 2x + 10

Report an Error

Example Question #142 : Geometry

A line segment has the endpoints (-1, 3) and (4,-2) . What is the length of this line segment?

Possible Answers:

$5\sqrt2$

$\sqrt{30}$

Correct answer:

$5\sqrt2$

Explanation:

Use the following formula to find the distance between two points:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Plug in the points that are given.

$\text{Distance}=\sqrt{(4-(-1))^2+(-2-3)^2}$

$\text{Distance}=\sqrt{(5)^2+(-5)^2}$

$\text{Distance}=\sqrt{25+25}=\sqrt{50}=\sqrt{5*5*2}=5\sqrt2$

Report an Error

Example Question #1 : How To Find The Length Of A Line With Distance Formula

A line segment has end points at (8,1) and (-2,-3) . What is the length of this line segment?

Possible Answers:

7.46

10.77

9.88

6.32

Correct answer:

10.77

Explanation:

The distance between two points is given by the following equation:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Now, using the two given points, plug them in to find the distance.

$\text{Distance}=\sqrt{(-2-8)^2+(-3-1)^2}=\sqrt{100+16}=\sqrt{116}=10.77$

Report an Error

Example Question #2 : How To Find The Length Of A Line With Distance Formula

Find the length of a line that has end points at $(8, -1)\text{ and }(-2, 1)$ .

Possible Answers:

126

104

$2\sqrt{26}$

$\sqrt{26}$

Correct answer:

$2\sqrt{26}$

Explanation:

Use the distance formula to find the length of this line segment:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Substitute in the values provided:

$\text{Distance}=\sqrt{(-2-8)^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}$

At this point, break down the square root:

$\sqrt{104}=\sqrt{2\cdot52}=\sqrt{2\cdot2\cdot26}=\sqrt{2\cdot2\cdot2\cdot13}$

You can remove two of the twos and put them on the outside of the square root symbol, and multiply the two and the thirteen that remain underneath the square root symbol:

$\sqrt{2\cdot2\cdot2\cdot13}=2\sqrt{2\cdot13}=2\sqrt{26}$

Report an Error

Example Question #3 : How To Find The Length Of A Line With Distance Formula

A line segment has endpoints at $(-2, -1)\text{ and }(8, 1)$ . Find the length of this line.

Possible Answers:

$6\sqrt{3}$

$2\sqrt{26}$

Correct answer:

$2\sqrt{26}$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

Where,

(x_1,y_1)=(-2,-1) and (x_2,y_2)=(8,1) .

$\text{Distance}=\sqrt{(8-(-2))^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}=2\sqrt{26}$

Report an Error

Example Question #371 : Ssat Upper Level Quantitative (Math)

Find the length of the line segment that has endpoints $(0, 4)\text{ and }(12, 6)$ .

Possible Answers:

12.412

10.659

12.166

8.451

Correct answer:

12.166

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

(x_1,y_1)=(0,4) and (x_2,y_2)=(12,6) .

$\text{Distance}=\sqrt{(12-0)^2+(6-4)^2}=\sqrt{144+4}=\sqrt{148}=12.166$

Report an Error

Example Question #151 : Geometry

Find the length of the line segment that has the endpoints $(2, 4)\text{ and }(7, 8)$ .

Possible Answers:

$\sqrt{29}$

$\sqrt{31}$

$\sqrt{41}$

Correct answer:

$\sqrt{41}$

Explanation:

Use the distance formula to find the length of the line.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

(x_1,y_1)=(2,4) and (x_2,y_2)=(7,8) .

$\text{Distance}=\sqrt{(7-2)^2+(8-4)^2}=\sqrt{25+16}=\sqrt{41}$

Report an Error

Example Question #1 : How To Find The Length Of A Line With Distance Formula

One leg of a triangle has endpoints at the coordinates $(-1, -2)\text{ and }(-4, -1)$ . Find the length of this leg.

Possible Answers:

$\sqrt{10}$

$2\sqrt2$

Correct answer:

$\sqrt{10}$

Explanation:

Use the distance formula to find the length of the leg.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

(x_1,y_1)=(-1,-2) and (x_2,y_2)=(-4,-1) .

$\text{Length}=\sqrt{(-4-(-1))^2+(-1-(-2))^2}=\sqrt{9+1}=\sqrt{10}$

Report an Error

View SSAT- Upper Level Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Thomas
Certified Tutor

Dartmouth College, Bachelor in Arts, Biochemistry and Molecular Biology. Columbia University in the City of New York, Master ...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Washington DC, SAT Tutors in Seattle, MCAT Tutors in Los Angeles, French Tutors in New York City, Biology Tutors in Denver, Statistics Tutors in New York City, ISEE Tutors in Washington DC, ISEE Tutors in Phoenix, Spanish Tutors in Chicago, GRE Tutors in Denver

Popular Courses & Classes

SSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in New York City, GMAT Courses & Classes in Houston, SSAT Courses & Classes in Washington DC, ACT Courses & Classes in New York City

Popular Test Prep

GMAT Test Prep in Chicago, ACT Test Prep in Houston, LSAT Test Prep in Los Angeles, GMAT Test Prep in Washington DC, GMAT Test Prep in Houston, SSAT Test Prep in Houston, MCAT Test Prep in Washington DC, SSAT Test Prep in Denver, ISEE Test Prep in Seattle, LSAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Coordinate Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Perpendicular Line

Example Question #2 : How To Find The Equation Of A Perpendicular Line

Example Question #441 : Geometry

Example Question #142 : Geometry

Example Question #1 : How To Find The Length Of A Line With Distance Formula

Example Question #2 : How To Find The Length Of A Line With Distance Formula

Example Question #3 : How To Find The Length Of A Line With Distance Formula

Example Question #371 : Ssat Upper Level Quantitative (Math)

Example Question #151 : Geometry

Example Question #1 : How To Find The Length Of A Line With Distance Formula

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: