SSAT Middle Level Math : SSAT Middle Level Quantitative (Math)
Study concepts, example questions & explanations for SSAT Middle Level Math
All SSAT Middle Level Math Resources
Example Questions
Example Question #21 : How To Find The Area Of A Rectangle
Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the ratio of the area of the red region to that of the white region.
The correct answer is not given among the other choices.
The large rectangle has length 80 and width 40, and, consequently, area
The white region is a rectangle with length 30 and width 20, and, consequently, area
The red region, therefore, has area 
The ratio of the area of the red region to that of the white region is
That is, 13 to 3.
Example Question #341 : Ssat Middle Level Quantitative (Math)
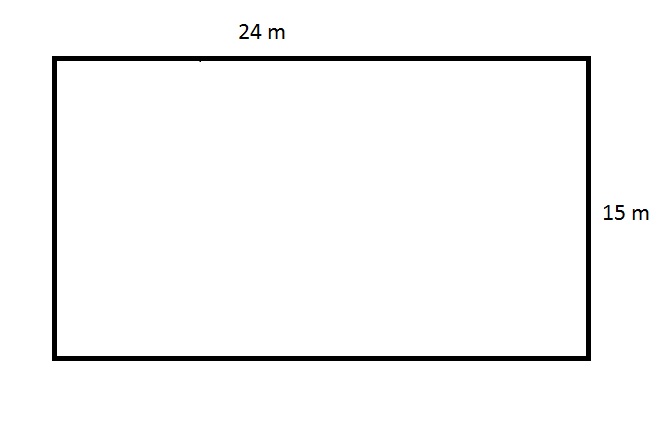
The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely, but the store will only sell the material in multiples of one hundred square meters. How many square meters will the manager need to buy?
Insufficient information is given to answer the question.
The tarp needed to cover this pool must be, at minimum, the product of its length and width, or
The manager will need to buy a number of square yards of tarp equal to the next highest multiple of one hundred, which is 400 square meters.
Example Question #111 : Plane Geometry
The four angles of a square are labeled A, B, C, and D. What is the sum of 
More information is needed to solve
In a square, each angle is 90 degrees.
We can plug in 90 for each variable and find the sum.
Example Question #24 : How To Find The Area Of A Rectangle
The above depicts a rectangular swimming pool for an apartment. The pool is six feet deep everywhere.
An apartment manager wants to paint the four sides and the bottom of the swimming pool. How many square feet will he need to paint?
The correct answer is not given among the other responses.
The bottom of the swimming pool has area
There are two sides whose area is
and two sides whose area is
Add the areas:
Example Question #25 : How To Find The Area Of A Rectangle
If the angles of a quadrilateral are equal to 
Given that there are 360 degrees in a quadrilateral,
Example Question #32 : How To Find The Area Of A Rectangle
What is the value of 
Given that there are 360 degrees in a quadrilateral,
Example Question #112 : Plane Geometry
If the length of a rectangle is 7.5 feet and the width is 2 feet, what is the value of 
The area of a rectangle is calculated by multiplying the length by the width. Here, the length is 7.5 and the width is 2, so the area will be 15.
Given that the area is also equal to 
Example Question #81 : Quadrilaterals
If a cereal box has a volume of 40 cubic inches, a width of 2 inches, and a height of 5 inches, what is its length?
The formula for the volume of a rectangular solid is 
Use the provided information from the question in the above formula and solve for the length.
Therefore, the length of the box is 4 inches. In answering this question, it is important to look at the units before selecting an answer. It is easy to be tricked into thinking that because the total answer is in cubic inches that it may be necessary to have square inches, but when multiplying three values, each with inches as their units, the units of the product will be cubic inches.
Example Question #342 : Ssat Middle Level Quantitative (Math)
One cubic meter is equal to one thousand liters.
The above depicts a rectangular swimming pool for an apartment. The pool is 
The pool can be seen as a rectangular prism with dimensions 
One cubic meter is equal to one thousand liters, so multiply:
Example Question #121 : Plane Geometry
Which of the following is equal to the area of a rectangle with length 
Multiply each dimension by 
Multiply these dimensions to get the area of the rectangle in square centimeters:
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources
