We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Quadrilaterals

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #193 : Geometry

Measured in units, the bases of a trapezoid are and , the lengths are , and the height is unknown. What is the perimeter of the trapezoid in units?

Possible Answers:

Impossible to calculate.

Correct answer:

Explanation:

The perimeter is solved by adding the two bases together, and , along with both the lengths, .

Therefore the equation becomes,

5+2+20+20=47

Report an Error

Example Question #194 : Geometry

Measured in units, the bases of a trapezoid are and , the lengths are , and the height is unknown. What is the perimeter of the trapezoid in units?

Possible Answers:

Impossible to calculate.

Correct answer:

Explanation:

The perimeter is solved by adding the two bases together, and , along with both the lengths, .

Therefore the equation becomes,

5+2+10+10=27

Report an Error

Example Question #201 : Geometry

Measured in units, the bases of a trapezoid are and , the lengths are , and the height is unknown. What is the perimeter of the trapezoid in units?

Possible Answers:

Impossible to calculate.

Correct answer:

Explanation:

The perimeter is solved by adding the two bases together, and , along with both the lengths, .

Therefore the equation becomes,

5+10+10+10=35

Report an Error

Example Question #155 : Plane Geometry

Measured in units, the bases of a trapezoid are and , the lengths are , and the height is unknown. What is the perimeter of the trapezoid in units?

Possible Answers:

Impossible to calculate

Correct answer:

Explanation:

The perimeter is solved by adding the two bases together, and , along with both the lengths, .

Therefore the equation becomes,

10+15+10+10=45

Report an Error

Example Question #11 : Trapezoids

Find the perimeter of the trapezoid:
Question_12

Possible Answers:

$\small 40$

$\small 21$

$\small 26$

$\small 23.5$

Correct answer:

$\small 21$

Explanation:

The perimeter of any shape is equal to the sum of the lengths of its sides:

$\small P=4+6+3+8=21$

Report an Error

Example Question #121 : Quadrilaterals

Trapezoid

Find the perimeter of the given trapezoid if $l=9, h=7, b_{1}=8, b_{2}=10$

Possible Answers:

Correct answer:

Explanation:

In order to find the perimeter, we must find the sum of the outer edges:

Trapezoid_labeled

9+8+ 9+10=36

Notice that we didn't use height in our calculation.

Report an Error

Example Question #121 : Quadrilaterals

Trapezoid

Find the perimeter of the given trapezoid if $l=6, h=4, b_{1}=2, b_{2}=5$

Possible Answers:

Correct answer:

Explanation:

In order to find the perimeter, find the sum of the outer edges:

Trapezoid_labeled

6+2+6+5=19

Notice that we didn't use height in our calculation.

Report an Error

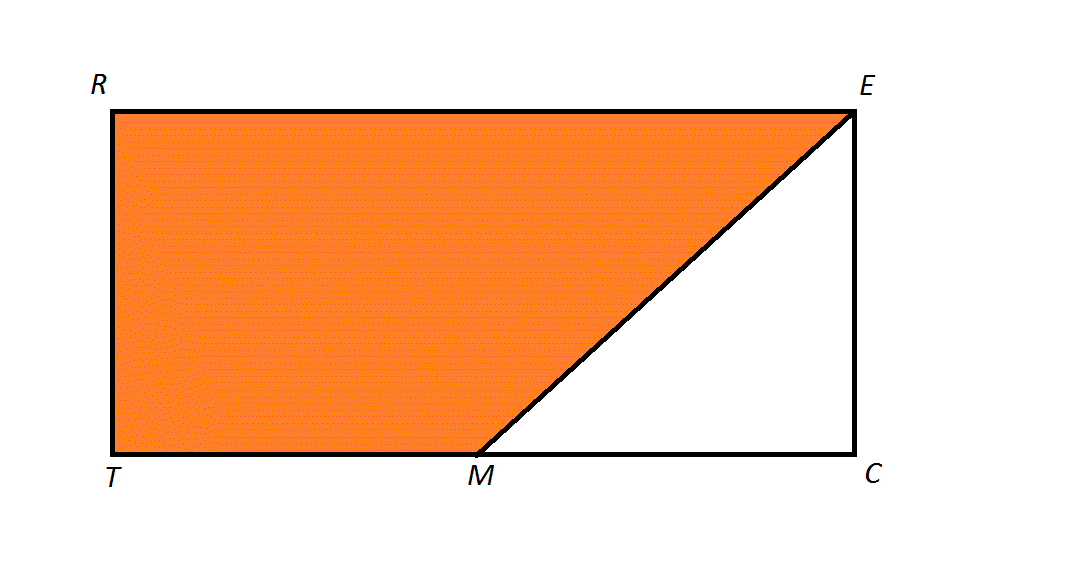
Example Question #1 : How To Find The Area Of A Trapezoid

Trapezoid

The above diagram depicts a rectangle RECT with isosceles triangle $\Delta ECM$ . is the midpoint of $\overline{CT}$ . What is the ratio of the area of the orange trapezoid to that of the white triangle?

Possible Answers:

More information is needed to answer this question.

4:1

3:1

7:2

9:2

Correct answer:

3:1

Explanation:

We can simplify this problem by supposing that the length of one leg of a triangle is 2. Then the other leg is 2, and the area of the triangle is

$A = \frac {1}{2} \cdot 2 \cdot 2 = 2$

Since is the midpoint of $\overline{CT}$ , MT = 2 . Also, since opposite sides of a rectangle are congruent,

RE = CT = CM + MT = 2 + 2 = 4 .

This makes the trapezoid one with height 2 and bases 2 and 4, so

$A = \frac {1}{2} \cdot (2 + 4) \cdot 2 = 6$

The ratio of the area of the trapezoid to that of the triangle is 6 to 2, which simplifies to 3 to 1.

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

Find the area of the trapezoid above.

Note: Image not drawn to scale.

Possible Answers:

$80\: cm$

$200\: cm^{2}$

$120\: cm^{2}$

$160\: cm$

$120\: cm$

Correct answer:

$120\: cm^{2}$

Explanation:

The area of a trapezoid is equal to the average of the length of the two bases multiplied by the height.

The formula to find the area of a trapezoid is: $\left (\frac{base_{1} + base_{2}}{2}\right )* height$

In this problem, the lengths of the bases are $10\: cm$ and $20\: cm.$ Their average is $15\: cm$ . The height of the trapezoid is $8\: cm.$

$15\: cm\ast 8\: cm=120\: cm$

Remember: the answer to the problem should have units in cm² .

Report an Error

Example Question #3 : How To Find The Area Of A Trapezoid

Find the area of a trapezoid with a height of $5\:cm$ and base lengths of $4\:cm$ and $8\:cm$ , respectively.

Possible Answers:

$17\:cm$

$15\:cm^{2}$

$22\:cm^{2}$

$30\:cm^{2}$

$10\:cm^{2}$

Correct answer:

$30\:cm^{2}$

Explanation:

The area of a trapezoid is equal to the average of its two bases ( $b_{1}$ and $b_{2}$ ) multiplied by its height . Therefore:

$A=\frac{1}{2}(b_{1}+b_{2})h$

$A=\frac{1}{2}(4\:cm+8\:cm)5\:cm$

$A=\(6\:cm)5\:cm$

$A=30\:cm^{2}$

Report an Error

View SSAT- Middle Level Tutors

Jason
Certified Tutor

NJCU, Bachelor in Arts, Communication, General. Saint Peters College, Masters in Business Administration, Elementary and Midd...

View SSAT- Middle Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Middle Level Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Miami, Spanish Tutors in Atlanta, English Tutors in Phoenix, LSAT Tutors in San Francisco-Bay Area, SAT Tutors in Philadelphia, SAT Tutors in Washington DC, Spanish Tutors in Houston, GMAT Tutors in Boston, MCAT Tutors in San Diego, LSAT Tutors in Los Angeles

Popular Courses & Classes

SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Seattle, GRE Courses & Classes in Boston, Spanish Courses & Classes in Philadelphia, ACT Courses & Classes in Phoenix, GRE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Boston, GRE Courses & Classes in Houston, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in Phoenix, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Miami, ACT Test Prep in Boston, LSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Los Angeles, SSAT Test Prep in San Diego, GMAT Test Prep in Atlanta, ACT Test Prep in Miami, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Quadrilaterals

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #193 : Geometry

Example Question #194 : Geometry

Example Question #201 : Geometry

Example Question #155 : Plane Geometry

Example Question #11 : Trapezoids

Example Question #121 : Quadrilaterals

Example Question #121 : Quadrilaterals

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #3 : How To Find The Area Of A Trapezoid

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: