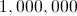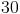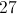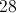The probability is expressed as the circumstance out of the whole number available.

The number of marbles that are red is 7, and the whole number of marbles is 20.

Therefore the probability is 

\(\displaystyle \frac{7}{20}\).

To find the probability of an event happening, we use the following

\(\displaystyle \text{probability of an event} = \frac{\text{number of ways it can happen}}{\text{total number of possible outcomes}}\)

So, if we look at the number of ways we can draw a Queen, we can come up with

• Queen of Hearts
• Queen of Diamonds
• Queen of Spades
• Queen of Clubs

So, the number of ways we can draw a queen is equal to 4.  So,

\(\displaystyle \text{probability of drawing a Queen} = \frac{4}{\text{total number of possible outcomes}}\)

Now, to find the total number of possible outcomes, we will think of how many different cards there are within a deck.  We know there are 52 total cards, which means there are 52 total possible outcomes.  So,

\(\displaystyle \text{probability of drawing a Queen} = \frac{4}{52}\)

Now, we can simplify.

\(\displaystyle \text{probability of drawing a Queen} = \frac{4}{52}\)

\(\displaystyle \text{probability of drawing a Queen} = \frac{2}{26}\)

\(\displaystyle \text{probability of drawing a Queen} = \frac{1}{13}\)

To find the probability of an event happening, we use the following

\(\displaystyle \text{probability of an event} = \frac{\text{number of ways it can happen}}{\text{total number of possible outcomes}}\)

To calculate the number of ways this can happen it is important to recall that each suit (Hearts, Clubs, Spades, and Diamonds) have one value for numbers 1 through 10, one jack, one queen, one queen, and one ace. Therefore there is only one card that is the 2 of Hearts.

So, the number of ways we can draw a 2 of Hearts is equal to 1.  So,

\(\displaystyle \text{probability of drawing a 2 of Hearts} = \frac{1}{\text{total number of possible outcomes}}\)

Now, to find the total number of possible outcomes, we will think of how many different cards there are within a deck.  We know there are 52 total cards, which means there are 52 total possible outcomes.  So,

\(\displaystyle \text{probability of drawing a 2 of Hearts} = \frac{1}{52}\)

To find the probability of an event, we will use the following formula:

\(\displaystyle \text{probability of event} = \frac{\text{number of ways event can happen}}{\text{total number of possible outcomes}}\)

So, given the event of drawing a 4, we can calculate the following:

\(\displaystyle \text{number of ways event can happen} = 4\)

Because there are 4 ways to draw a 4 from a deck of cards:

• 4 of Hearts
• 4 of Diamonds
• 4 of Clubs
• 4 of Spades

Now, we can calculate the following:

\(\displaystyle \text{total number of possible outcomes} = 52\)

Because there are 52 cards we could potentially draw from a deck of cards.

Knowing this, we can substitute into the formula.  We get

\(\displaystyle \text{probability of drawing 4} = \frac{4}{52}\)

\(\displaystyle \text{probability of drawing 4} = \frac{2}{26}\)

\(\displaystyle \text{probability of drawing 4} = \frac{1}{13}\)

Therefore, the probability of drawing a 4 from a deck of cards is \(\displaystyle \frac{1}{13}\).

To find the probability of an event, we will use the following formula:

\(\displaystyle \text{probability of event} = \frac{\text{number of ways event can happen}}{\text{total number of possible outcomes}}\)

So, given the event of the teacher calling on a girl, we can calculate the following:

\(\displaystyle \text{number of ways event can happen} = 11\)

Because there are 11 girls in the classroom.

Now, we can calculate the following:

\(\displaystyle \text{total number of possible outcomes} = 26\)

Because there are 26 total students the teacher could potentially call on.

Knowing this, we can substitute into the formula.  We get

\(\displaystyle \text{probability of calling on a girl} = \frac{11}{26}\)

Therefore, the probability of the teacher calling on a girl is \(\displaystyle \frac{11}{26}\).

To find the probability of an event, we will use the following formula:

\(\displaystyle \text{probability of event} = \frac{\text{number of ways event can happen}}{\text{total number of possible outcomes}}\)

So, given the event of drawing a 3, we can calculate the following:

\text{number of ways event can happen} = 4

Because there are 4 ways we can draw a 3 from the deck:

• 3 of clubs
• 3 of spades
• 3 of diamonds
• 3 of hearts

Now, we can calculate the following:

 \text{total number of possible outcomes} = 52

Because there are 52 cards we could potentially draw from a deck of cards.

Knowing this, we can substitute into the formula.  We get

\(\displaystyle \text{probability of drawing a 3} = \frac{4}{52}\)

\(\displaystyle \text{probability of drawing a 3} = \frac{2}{26}\)

\(\displaystyle \text{probability of drawing a 3} = \frac{1}{13}\)

Therefore, the probability of drawing a 3 from a deck of cards is \(\displaystyle \frac{1}{13}\).

The set of whole numbers comprises the following:

\(\displaystyle \left \{ 0, 1, 2, 3, 4, 5...\right \}\)

All of the given choices are members of this set.

Each entry in the sequence is obtained by adding to the previous entry a number that increases by 1 each time.

\(\displaystyle 2 + 2 = 4\)

\(\displaystyle 4+3 = 7\)

\(\displaystyle 7+4=11\)

\(\displaystyle 11+5=16\)

\(\displaystyle 16+6=22\)

To get the next entry, add 7.

\(\displaystyle 22+7= 29\)

The set is increasing. To figure out by how much, simply subtract any two numbers in the set, but remember to put the greater number first!

Example: \(\displaystyle 2.3 -1.2 =1.1\)

Each number in the set increases by 1.1. To find the missing part of this set, add 1.1 to the number just before the blank.

\(\displaystyle 1.1 +3.4 = 4.5\)

The complete set is: 1.2, 2.3, 3.4, 4.5, 5.6.

First, you must notice that the set is increasing. When you look at how all the numbers are related, you will notice that this is a “growing” set, meaning the difference between each number in the set is increasing. To figure out by how much, simply subtract any two numbers in the set.

When you subtract the first two numbers in the set, you will get: \(\displaystyle 7-6=1\).

If you subtract the next two numbers, you will get: \(\displaystyle 9-7=2\).

Then the next two: \(\displaystyle 10-7=3\).

Now you can see a pattern. Each number increases by 1, 2, 3, and so on.

\(\displaystyle 6(+1),\ 7(+2),\ 9(+3),\ 12(+4),\ 16(+5),\ 21(+6),\ ?,\ 34\)

To find the missing number in the set, we must add 6 to 21.

\(\displaystyle 21+6=27\)

Now we can see the complete set.

\(\displaystyle 6(+1),\ 7(+2),\ 9(+3),\ 12(+4),\ 16(+5),\ 21(+6),\ 27(+7),\ 34\)