The domain of f(x) is defined as all of the values of x for which f(x) is defined.

The first value we have to consider is 1. Let's find f(1):

f(1) = (1³ – 3(1)² +2(1))^–1

= (1 – 3(1) + 2)^–1

= (1 – 3 + 2)^–1

= (0)^–1.

Remember that, in general, a^–1 = 1/a. Thus, 0^–1 = 1/0. However, it is impossible to have 0 in the denominator of a fraction, because it is impossible to divide anything by zero. Thus, 0^–1 is undefined. Since f(1) is undefined, 1 cannot belong to the domain of f(x).

Now let's find f(2):

f(2) = (2³ – 3(2)² +2(2))^–1

= (8 – 3(4) + 4)^–1

=(8 – 12 + 4)^–1

= 0^–1

Because f(2) is undefined, 2 is not in the domain of f(x).

Finally, we can look at f(–1):

f(–1) = ((–1)³ – 3(–1)² +2(–1))^–1

= (–1 – 3(1) – 2)^–1

= (–1 – 3 – 2)^–1 = (–6)^–1 = –1/6.

f(–1) is defined, so –1 belongs to the domain of f(x).

Therefore only III is in the domain of f(x).

The domain of f(x) is all the values of x for which f(x) is defined.

f(x) has no square roots or denominators, so it will always be defined; there are no restrictions on x because any and all values will lead to a real result.

Therefore, the domain is the set of all real numbers.

Using our properties of exponents, we could rewrite  as  

This means that when we input , we first subtract 2, then take this to the fourth power, then take the fifth root, and then add three. We want to look at these steps individually and see whether there are any values that wouldn’t work at each step. In other words, we want to know which  values we can put into our function at each step without encountering any problems.

The first step is to subtract 2 from . The second step is to take that result and raise it  to the fourth power. We can subtract two from any number, and we can take any number to the fourth power, which means that these steps don't put any restrictions on .

Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function  is defined for any value of ; thus the fact that  has a fifth root in it doesn't put any restrictions on , because we can add three to any number; therefore, the domain for  is all real values of .

The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.

When x = 0 or x = 3, the function is undefined due to its denominator. 

Thus the domain is all real numbers x, such that x is not equal to 0 or 3.

If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into

and then cancelling the 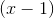 from the numerator and the denominator. 

This new expression,  is the equation of the function, but it will have a hole at the point where the denominator originally would have been zero. Thus, this graph will look like the line  with a hole where , which is 

.

Thus the domain of the function is all  values such that 

The purpose of this question is to understand when x values will yield y values. The term inside of a square root can be positive or equal to zero in order to yield a value. This means that x can be equal to all real numbers that are -9 or higher, which shows that the domain of the function is all real numbers that are at least -9.

For the square root of a function to be defined on the real numbers, the radicand must be nonnegative. Therefore, 

, or .

Any nonnegative number can be the radicand, so  has no lower bound. This makes the natural domain 

The key here is to factor the denominator, bearing in mind that once we do, we can find the values for which the denominator will be and therefore the values for which the function will not be valid.

We can thus deduce from those three factors that the function will not be valid when .

The domain of a function is all values that you can put in for x without breaking any rules. When first approaching this problem, you must realize that when dealing with a fraction, the denominator can never be 0. Thus, any x value that makes the denominator 0 must be removed from our domain set. Thus,

Since x=3 will make our denominator 0, it must be removed. All other values are permitted, so our answer is