SAT Math : How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #92 : Plane Geometry
If a 18-foot light pole casts a shadow of 7 feet on even ground, what is the distance from the top of the light pole to the top of it’s shadow?
First, you will want to draw a small diagram to help you:
After looking at the diagram, it is clear this is a right triangle problem where we can use the Pythagorean Theorem (a2 + b2 = c2 ).
The distance from the top of the light pole to the top of it’s shadow is 19.31 feet.
Process of Elimination Hint: You can immediate eliminate 2 answers based on the properties of right triangles. The hypotenuse has to be longer than either one of the other two sides (must be greater than 18 ft) and less than the length of the other two sides added together (must be less than 25 feet). Therefore, 17.78 feet and 25.12 feet are unreasonable answers.
Example Question #71 : Triangles
The above figure shows Square 
Since all four sides of a square are congruent,
Since 
Since 
and
Substituting:
Apply the Product of Radicals and Quotient of Radicals Rules:
Example Question #94 : Plane Geometry
In a right triangle, the lengths of the two smallest sides are 5 and 12. Find the length of the hypotenuse.
In order to find the length of the hypotenuse, we need to use the pythagorean theorem, which states that
By substituting 5 for a and 12 for b, we get
or,
To solve for c we need to take the square root of 169, which is 13. Therefore, the hypotenuse is 13.
Example Question #81 : Triangles
Susie walks north from her house to a park that is 30 meters away. Once she arrives at the park, she turns and walks west for 80 meters to a bench to feed some pigeons. She then walks north for another 30 meters to a concession stand. If Susie returns home in a straight line from the concession stand, how far will she walk from the concession stand to her house, in meters?
100
50
70
25
200
100
Susie walks 30 meters north, then 80 meters west, then 30 meters north again. Thus, she walks 60 meters north and 80 meters west. These two directions are 90 degrees away from one another.
At this point, construct a right triangle with one leg that measures 60 meters and a second leg that is 80 meters.
You can save time by using the 3:4:5 common triangle. 60 and 80 are 
We can solve for the length of the missing hypotenuse by applying the Pythagorean theorem:
Substitute the following known values into the formula and solve for the missing hypotenuse: side 
Susie will walk 100 meters to reach her house.
Example Question #82 : Triangles
The lengths of the sides of a triangle are consecutive odd numbers and the triangle's perimeter is 57 centimeters. What is the length, in centimeters, of its longest side?
17
25
19
23
21
21
First, define the sides of the triangle. Because the side lengths are consecutive odd numbers, if we define the shortest side will be as 
Substitute in the known values and variables.
Subtract 6 from both sides of the equation.
Divide both sides of the equation by 3.
Solve.
This is not the answer; we need to find the length of the longest side, or 
Substitute in the calculated value for 
The longest side of the triangle is 21 centimeters long.
Example Question #1324 : Basic Geometry
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
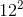
All SAT Math Resources
