All SAT Math Resources
Example Questions
Example Question #1 : Cubes
What is the length of the diagonal of a cube with volume of 512 in3?
None of the other answers
2√(6) in
8√(3) in
8 in
4√(3) in
8√(3) in
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = s3, where s is the length of the cube. For our data, this is:
s3 = 512, or (taking the cube root of both sides), s = 8.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (8,8,8). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √( (x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
Or for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (8)2 + (8)2 + (8)2) = √( 64 + 64 + 64) = √(64 * 3) = 8√(3)
Example Question #1 : Cubes
What is the length of the diagonal of a cube with volume of 1728 in3?
12 in
18 in
3√(3) in
6√(3) in
12√(3) in
12√(3) in
The first thing necessary is to determine the dimensions of the cube. This can be done using the volume formula for cubes: V = s3, where s is the length of the cube. For our data, this is:
s3 = 1728, or (taking the cube root of both sides), s = 12.
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (12,12,12). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean theorem):
d = √( (x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
Or, for our simpler case:
d = √( (x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (12)2 + (12)2 + (12)2) = √( 144 + 144 + 144) = √(3 * 144) = 12√(3) = 12√(3)
Example Question #1 : How To Find The Diagonal Of A Cube
What is the length of the diagonal of a cube with surface area of 294 in2?
None of the other answers
21√(2)
7√(3)
14
21
7√(3)
The first thing necessary is to determine the dimensions of the cube. This can be done using the surface area formula for cubes: A = 6s2, where s is the length of the cube. For our data, this is:
6s2 = 294
s2 = 49
(taking the square root of both sides) s = 7
The distance from corner to corner of the cube will be equal to the distance between (0,0,0) and (7,7,7). The distance formula for three dimensions is very similar to that of 2 dimensions (and hence like the Pythagorean Theorem):
d = √((x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
Or for our simpler case:
d = √((x)2 + (y)2 + (z)2) = √( (s)2 + (s)2 + (s)2) = √( (7)2 + (7)2 + (7)2) = √( 49 + 49 + 49) = √(49 * 3) = 7√(3)
Example Question #701 : Geometry
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
Example Question #2 : Cubes
What is the surface area of a cube with a volume of 1728 in3?
432 in2
72 in2
1728 in2
144 in2
864 in2
864 in2
This problem is relatively simple. We know that the volume of a cube is equal to s3, where s is the length of a given side of the cube. Therefore, to find our dimensions, we merely have to solve s3 = 1728. Taking the cubed root, we get s = 12.
Since the sides of a cube are all the same, the surface area of the cube is equal to 6 times the area of one face. For our dimensions, one face has an area of 12 * 12 or 144 in2. Therefore, the total surface area is 6 * 144 = 864 in2.
Example Question #701 : Geometry
A room has dimensions of 18ft by 15ft by 9ft. The last dimension is the height of the room. It has one door that is 3ft by 7ft and two windows, each 2ft by 5ft. There is no trim to the floor, wall, doors, or windows. What is the total exposed wall space?
553 ft2
1134ft2
594 ft2
1093ft2
2389ft2
553 ft2
If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 9 ft high, we know 18 x 15 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 18 x 9 and 15 x 9. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:
2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 ft2
Now, we merely need to calculate the area "taken out" of the walls:
For the door: 3 * 7 = 21 ft2
For the windows: 2 * (2 * 5) = 20 ft2
The total wall space is therefore: 594 – 21 – 20 = 553 ft2
Example Question #1 : How To Find The Surface Area Of A Cube
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
750
100
500
1000
200
750
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6s2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to s3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
Example Question #1 : How To Find The Surface Area Of A Cube
A company wants to build a cubical room around a cone so that the cone's height and diameter are 3 inch less than the dimensions of the cube. If the volume of the cone is 486π ft3, what is the surface area of the cube?
69,984 in2
513.375 in2
726 in2
486 in2
73,926 in2
73,926 in2
To begin, we need to solve for the dimensions of the cone.
The basic form for the volume of a cone is: V = (1/3)πr2h
Using our data, we know that h = 2r because the height of the cone matches its diameter (based on the prompt).
486π = (1/3)πr2 * 2r = (2/3)πr3
Multiply both sides by (3/2π): 729 = r3
Take the cube root of both sides: r = 9
Note that this is in feet. The answers are in square inches. Therefore, convert your units to inches: 9 * 12 = 108, then add 3 inches to this: 108 + 3 = 111 inches.
The surface area of the cube is defined by: A = 6 * s2, or for our data, A = 6 * 1112 = 73,926 in2
Example Question #321 : Geometry
If the volume of a cube is 216 cubic units, then what is its surface area in square units?
54
216
36
108
64
216
The volume of a cube is given by the formula V = 
In order to find s, we can find the cube root of both sides of the equaton. Finding the cube root of a number is the same as raising that number to the one-third power.
This means the length of the side of the cube is 6. We can use this information to find the surface area of the cube, which is equal to 

surface area =
The surface area of the square is 216 square units.
The answer is 216.
Example Question #701 : Geometry
You have a cube with sides of 4.5 inches. What is the surface area of the cube?
The area of one side of the cube is:
A cube has 6 sides, so the total surface area of the cube is
All SAT Math Resources

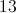










![\sqrt[3]{216}= 216^{1/3}=6=s](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/17880/gif.latex)











