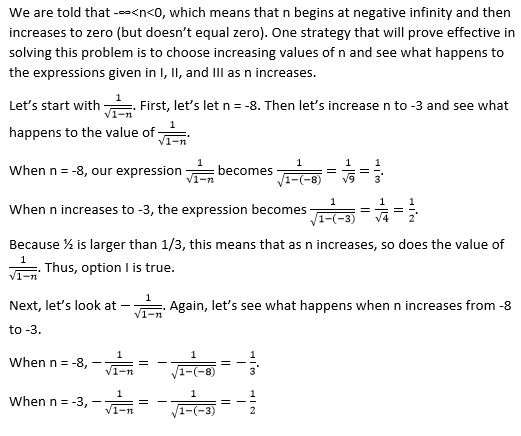Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Arithmetic

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Fractions

Which of the following has the greatest value?

Possible Answers:

4/7

5/8

52%

65%

Correct answer:

65%

Explanation:

If all are converted to decimals, 0.65 is the biggest.

Report an Error

Example Question #3 : Fractions

Which fraction falls between ½ and 3/4?

Possible Answers:

1/3

3/6

6/8

5/8

4/5

Correct answer:

5/8

Explanation:

The easiest method is to put each of these fractions into a calculator, and then place them in order on a number line to see which value falls in between 1/2 = 0.5 and ¾ = 0.75. Without a calculator you must do long division to find the value of the numerator (top number) divided by the denominator (bottom number) for each fraction. You can actually eliminate answers b. and d. because they are equal to 1/2 and ¾ respectively. 4/5= 0.80, 3/6 = 0.5, 5/8= 0.625, 6/8 = 0.75.

Report an Error

Example Question #1 : How To Order Fractions From Least To Greatest Or From Greatest To Least

If Ben is taller than Jaime, Mary is taller than Ben, and Chris is taller than Mary. Who is the second tallest?

Possible Answers:

Mary

Jaime

Ben

Chris

Not possible to tell

Correct answer:

Mary

Explanation:

Using math symbols to dictate height we find that Ben>Jaime, Mary>Ben, Chris>Mary. Putting these in order we have Chris>Mary, Mary>Ben, Ben>Jaime. This shows that Mary is the second tallest.

Report an Error

Example Question #1 : Fractions

Order the following fractions in descending order.

¹/₂, ²/₃, ²/₅, ³/₄, ⁴/₇

Possible Answers:

²/₃, ⁴/₇, ³/₄, ¹/₂, ²/₅

³/₄, ²/₃, ⁴/₇, ¹/₂, ²/₅

²/₅, ¹/₂, ⁴/₇, ²/₃, ³/₄

²/₅, ¹/₂, ³/₄, ⁴/₇, ²/₃

¹/₂, ²/₃, ²/₅, ³/₄, ⁴/₇

Correct answer:

³/₄, ²/₃, ⁴/₇, ¹/₂, ²/₅

Explanation:

Method 1:

Find the common denominator (420) and convert each fraction to this denominator:

¹/₂ = 210/420

²/₃ = 280/420

²/₅ = 168/420

³/₄ = 315/420

⁴/₇ = 240/420

Now sort by numerator, largest to smallest.

Method 2:

Divide each fraction to obtain a decimal. Sort the decimals, largest to smallest.

Report an Error

Example Question #1 : Fractions

Increasing_n1

Possible Answers:

I and II only

II and III only

II only

I only

I and III only

Correct answer:

I and III only

Explanation:

Increasing_n2

Increasing_n4

Report an Error

Example Question #1 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Which of the following fractions is between 0.2 and 0.3?

Possible Answers:

$\dpi{100} \small \frac{2}{3}$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small \frac{1}{4}$

$\dpi{100} \small \frac{1}{3}$

$\dpi{100} \small \frac{1}{6}$

Correct answer:

$\dpi{100} \small \frac{1}{4}$

Explanation:

$\dpi{100} \small \frac{1}{4}=0.25$

$\dpi{100} \small 0.2<0.25<0.3$

$\dpi{100} \small \frac{1}{6}\approx 0.167<0.2$

The other three choices are larger than 0.3.

Report an Error

Example Question #2 : Fractions

Which of the following fractions is the greatest?

Possible Answers:

$\frac{2}{3}$

$\frac{3}{4}$

$\frac{7}{10}$

$\frac{20}{23}$

$\frac{25}{28}$

Correct answer:

$\frac{25}{28}$

Explanation:

The trick to this problem is to see that three of the choices have the numerator and denominator 3 units apart. The other two choices can be made three units apart as well- multiply both $\frac{3}{4}$ and $\frac{2}{3}$ by $\frac{3}{3}$ to get them to be $\frac{9}{12}$ and $\frac{6}{9}$ , respectively.

The trick is that once all fractions are the same units apart in denominator and numerator, the biggest number is the largest fraction.

Report an Error

Example Question #3 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Order the following from least to greatest: three-fifths, seven-eighths, 0.5, sixteen-eighteenths, 97%, 17-fifths.

Possible Answers:

0.5 , three-fifths, seven-eighths, sixteen-eighteenths, -fifths, $97\%$

0.5 , three-fifths, seven-eighths, sixteen-eighteenths, $97\%$ , -fifths

0.5 , $97\%$ , three-fifths, seven-eighths, sixteen-eighteenths, -fifths

three-fifths, 0.5 , $97\%$ , seven-eighths, sixteen-eighteenths, -fifths

0.5 , three-fifths, sixteen-eighteenths, seven-eighths, $97\%$ , -fifths

Correct answer:

0.5 , three-fifths, seven-eighths, sixteen-eighteenths, $97\%$ , -fifths

Explanation:

We need to order: three fifths, seven eights, 0.5, sixteen eighteenths, 97%, seventeen fifths.

Let us re-write each as a fraction: $\frac{3}{5}$ , $\frac{7}{8}$ , $\frac{1}{2}$ , $\frac{16}{18}=\frac{8}{9}$ , $\frac{97}{100}$ , and $\frac{17}{5}$ . We can now easily order these:

$\frac{1}{2},\frac{3}{5},\frac{7}{8},\frac{8}{9},\frac{97}{100},\frac{17}{5}$

Report an Error

Example Question #5 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Which of the following fractions is less than $\frac{3}{8}$ ?

Possible Answers:

$\frac{1}{3}$

$\frac{1}{2}$

$\frac{4}{7}$

$\frac{6}{16}$

$\frac{5}{13}$

Correct answer:

$\frac{1}{3}$

Explanation:

The purpose of this question is to find understandable values of fractions, which must be done using a common scale. Since looking at the denominators in the answers shows that there are many different numbers, decimal values would be easier to use.

The decimal equivalencies are as follows:

$\frac{6}{16}=0.375$

$\frac{4}{7}=0.571$

$\frac{1}{2}=0.5$

$\frac{5}{13}=0.385$

$\frac{1}{3}=0.333$

Therefore, we know that $\frac{3}{8}$ is equal to 0.375 and find that the fraction that is less than that is $\frac{1}{3}$ , which is equal to 0.333 .

Report an Error

Example Question #11 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Order the following fractions from least to greatest:

$\frac{1}{6}, \frac{5}{7}, \frac{1}{3}, \frac{5}{6}$

Possible Answers:

$\frac{5}{7}, \frac{1}{6}, \frac{1}{3}, \frac{5}{6}$

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

$\frac{1}{3}, \frac{1}{6}, \frac{5}{6}, \frac{5}{7}$

$\frac{1}{6}, \frac{5}{7}, \frac{1}{3}, \frac{5}{6}$

$\frac{5}{6}, \frac{5}{7}, \frac{1}{3}, \frac{1}{6}$

Correct answer:

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

Explanation:

To solve this problem, let's find the least common denominator for our fractions.

$7\cdot6 = 42$

is the lowest number that each of our current denominators are factors of.

Now, let's rewrite each fraction so that its denominator is .

$\frac{1 \cdot 7}{6 \cdot7}, \frac{5\cdot6}{7\cdot6}, \frac{1\cdot14}{3 \cdot 14}, \frac{5\cdot7}{6\cdot7} = \frac{7}{42}, \frac{30}{42}, \frac{14}{42}, \frac{35}{42}$

Then we can rearrange these new fractions from least to greatest, keeping in mind what they're reduced forms were.

$\frac{7}{42}, \frac{14}{42}, \frac{30}{42}, \frac{35}{42}$

Then, by either simplifying these fractions or by remembering their original forms, we can see that the order of our fractions from least to greatest is:

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

Report an Error

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Kelly
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Economics.

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Houston, LSAT Courses & Classes in Denver, LSAT Courses & Classes in San Diego, GRE Courses & Classes in Houston, GMAT Courses & Classes in New York City, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Chicago, GRE Courses & Classes in New York City, SSAT Courses & Classes in Houston, Spanish Courses & Classes in Los Angeles

Popular Test Prep

ACT Test Prep in Philadelphia, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Diego, SAT Test Prep in Los Angeles, ACT Test Prep in Houston, ISEE Test Prep in New York City, SSAT Test Prep in Houston, GRE Test Prep in Denver, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Arithmetic

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : Fractions

Example Question #3 : Fractions

Example Question #1 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Example Question #1 : Fractions

Example Question #1 : Fractions

Example Question #1 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Example Question #2 : Fractions

Example Question #3 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Example Question #5 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Example Question #11 : How To Order Fractions From Least To Greatest Or From Greatest To Least

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: