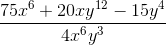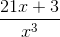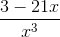SAT Math : Algebra
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #8 : Rational Expressions
Evaluate and simplify the following product:
The procedure for multplying together two rational expressions is the same as multiplying together any two fractions: find the product of the numerators and the product of the denominators separately, and then simplify the resulting quotient as far as possible, as shown:
Example Question #3 : Rational Expressions
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Example Question #275 : New Sat
Simplify the following rational expression:
Since both fractions in the expression have a common denominator of 
Example Question #5 : How To Add Rational Expressions With A Common Denominator
Simplify the following rational expression:
Since both rational terms in the expression have the common denominator 
Example Question #4 : How To Add Rational Expressions With A Common Denominator
Simplify the following expression:
Since both terms in the expression have the common denominator 
Example Question #2 : Evaluating And Simplifying Expressions
A total of 150 million votes were tallied in a presidential election. Votes were cast for either Hillary Clinton, Rand Paul, Al Gore, or Gary Johnson. If Clinton received 3 times the number of votes as Johnson, Paul received 30% of the vote, and Gore receieved 30 million total votes, who received the most votes in the election?
Rand Paul
Al Gore
Hillary Clinton
Gary Johnson
Hillary Clinton
There are a few ways to do this problem, but we will focus on the total number of votes method as follows. First, let Clinton = C, Gore = G, Paul = P, and Johnson = J. We know C + G + P + J = 150 million. We also know that C = 3J. Paul received 30% of the vote which is 150,000,000 * .3 = 45 million votes. Gore received 30 million votes. We can now create an equation with individual totals and substitute 3J for Clinton's vote total:
3J + 30 million + 45 million + J = 150 million
4J = 75 million
J = 18.75 million
Then C = 3J = 56.25 million. So Clinton received 56.25 million votes, Paul received 45 million votes, Gore received 30 million votes, and Johnson received 18.75 million votes. The correct answer is Hillary Clinton.
Example Question #3 : How To Evaluate Algebraic Expressions
Justin makes 61.9% of his free throws. During the season he had 84 free throw attempts. How many of Jason’s shots did not go in?
32
52
40
21
36
32
Find how many free throws Justin made: 84 x 0.619 = 51.99. Since the problem talks free throws, we round to 52 shots went in. To calculate shots missed:
84 – 52 = 32.
Example Question #4 : How To Evaluate Algebraic Expressions
If 5x + 30 = 6 – 7x, then x = ?
x = –18
x = –37
x = –10
x = 2
x = –2
x = –2
Combine like terms by subtracting 6 from both sides so: 5x + 24 = –7x. Then subtract 5x from both sides: 24 = –12x. Divide both sides by –12 and x = –2.
Example Question #4 : Evaluating Expressions
If ab - bc + d = d2 - c2, then what is the value of a when b is two, c is negative one, and d is zero?
ab - bc + d = d2 - c2
We need to substitute values in for b, c, and d, and then solve the equation for a.
a(2) - 2(-1) + 0 = 02 - (-1)2
2a +2 + 0 = 0 - (1)
2a + 2 = -1
2a = -3
a = -3/2
The answer is -3/2.
Example Question #5 : Evaluating Expressions
If 11x + 4 = 19x – 12, then what is 2x – 4?
Not possible
–8
0
2
4
0
First solve for x. The first equation would simplify as:
16 = 8x
x = 2
If we plug x = 2 into the second expression:
2(2) – 4 = 0
0 is the correct answer.
Certified Tutor
All SAT Math Resources
