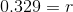Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Algebra

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1121 : Algebra

Solve for .

$3r+5t=\frac{-4Q+5z}{2}$

Possible Answers:

$Q=\frac{6r+10t+5z}{4}$

$Q=\frac{6r+10t+5z}{-4}$

$Q=\frac{6r+10t-5z}{-4}$

$Q=\frac{6r+10t-z}{-4}$

Correct answer:

$Q=\frac{6r+10t-5z}{-4}$

Explanation:

$3r+5t=\frac{-4Q+5z}{2}$

Multiply by on each side

2(3r+5t)=-4Q+5z

Expand right side

6r+10t=-4Q+5z

Subtract on each side

-4Q=6r+10t-5z

Divide by on each side

$Q=\frac{6r+10t-5z}{-4}$

Report an Error

Example Question #1122 : Algebra

If a rocket is shot from the ground, and it takes $5 \sec$ to reach a height of $500\:\text{m}$ . Determine the equation of its trajectory.

Possible Answers:

y=50x

y=100x

y=-100x

y=500x

y=10x

Correct answer:

y=100x

Explanation:

To figure out what the equation is, we need to use the point-slope form.

y-y_0=m(x-x_0) , where is the slope, and (x_0, y_0) is a point.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

In this example, y_2=500, y_1=0, x_2=5, x_1=0

$\text{Slope}=\frac{500-0}{5-0}=100$

y-0=100(x-0)

y=100x

Report an Error

Example Question #1123 : Algebra

Screen shot 2016 02 18 at 1.42.15 pm

Determine the x-intercepts in the graph above.

Possible Answers:

Not enough information

Correct answer:

Explanation:

The x-intercepts are the points on the graph where the y=0 line touches or intersects the x axis. By looking at the graph, there are two points. One at x=2 , and then another one at x=3 . So there are two x intercepts.

Report an Error

Example Question #1124 : Algebra

Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?

Possible Answers:

$33 \%$

$16.8 \%$

$13.29 \%$

$3.2 \%$

$168 \%$

Correct answer:

$33 \%$

Explanation:

Use the formula for exponential growth y = A*(1+r)^t where y is the current value, A is the initial value, r is the rate of growth, and t is time. Between 1997 and 2015, 18 years passed, so use t=18 . The stuffed animal was originally worth $6, so A=6 . It is now worth $1,015, so y=1015 .

Our equation is now:

$1015 = 6*(1+r)^{18}$ divide by 6:

$169.1\overline{6}=(1+r)^{18}$ take both sides to the power of $\frac{1}{18}=0.0\overline{5}$ :

$1.329 \approx 1+r$ subtract 1

0.329 = r

As a percent, r is about 33%.

Report an Error

Example Question #1124 : Algebra

The population of a city will decrease by 15 percent every 50 years and the population starts at 120,000 people. Construct a function that describes this situation.

Possible Answers:

$P(t)=120,000(0.85)^{50t}$

$P(t)=120,000(0.85)^{\frac{t}{50}}$

$P(t)=120,000(0.15)^{\frac{t}{50}}$

$P(t)=120,000(0.80)^{\frac{t}{50}}$

P(t)=120,000(0.85)^t

Correct answer:

$P(t)=120,000(0.85)^{\frac{t}{50}}$

Explanation:

To construct a function that describes this situation first identify what is known.

Since this particular situation is talking about population decrease, the function will be an exponential decay.

Recall that an exponential decay function is in the form,

$P(t)=I(1-r)^{t}$

where,

$\\P(t)=\text{ Finial population} \\I=\text{ Initial population} \\r=\text{ Rate} \\t=\text{Time}$

Since the statements says that the population decreases every 50 years we can rewrite the general form to,

$P(t)=I(1-r)^{\frac{t}{50}}$

Now substituting in the known values, the function can be written.

$P(t)=120,000(0.85)^{\frac{t}{50}}$

Report an Error

Example Question #1125 : Algebra

Screen shot 2016 02 18 at 2.50.12 pm

The above graph shows supply and demand for a particular Product. What is the equation for the demand of this product?

Possible Answers:

y=4x+50

y=-4x+50

y=2x+50

y=-2x+50

y=-4x

Correct answer:

y=-4x+50

Explanation:

We can determine the demand equation by using point slope form.

Point slope form is y-y_0=m(x-x_0) , where (x_0, y_0) , and is the slope, where $m=\frac{y_2-y_1}{x_2-x_1}$ .

Let y_2=50 , y_1=10 , x_2=0 , and x_1=10 .

$m=\frac{50-10}{0-10}=-4$

Now we have

y-y_0=-4(x-x_0)

Choose a point (0,50) ,

y-50=-4(x-0)

y=-4x+50

Report an Error

Example Question #1126 : Algebra

Screen shot 2016 02 18 at 2.50.12 pm

If the equation of the demand line is y=-4x+50 , and the equation for supply is y=5x , determine the point where supply and demand is the same.

Possible Answers:

$x=\frac{50}{9}$

$x=\frac{14}{9}$

x=6

$x=\frac{5}{9}$

$x=\frac{500}{9}$

Correct answer:

$x=\frac{50}{9}$

Explanation:

To solve this, all we need to do is set the equations equal to each other.

-4x+50=5x

Now solve for

50=9x

$x=\frac{50}{9}$

Report an Error

Example Question #1127 : Algebra

Amanda has 5000 ants in an ant farm and their population grows $20\%$ annually. How many ants will be in Amanda's ant farm in 6 years?

Possible Answers:

14920

14700

14930

14900

15000

Correct answer:

14930

Explanation:

This is an exponential growth problem, so let's recall the equation for exponential growth.

P(t)=P(1+r)^t , where is the starting amount of ants, is the growth rate, and is the time in years.

First step is to convert $20\%$ into a decimal. $20\%=0.20$

P(t)=5000(1+0.20)^t

P(t)=5000(1.20)^t

P(6)=5000(1.20)^6=14930

So in 6 years, Amanda will have 14930 ants.

Report an Error

Example Question #1128 : Algebra

The equation for the universal gravitation is $F_g=\frac{Gm_1m_2}{r^2}$ , $m_1=\text{mass of object 1}$ , $m_2=\text{mass of object 2}$ , $r=\text{radius between masses}$ , and is the universal gravitational constant. If $m_1=10 \ kg$ , $m_2=20 \ kg$ , $F_g=1.34\times10^{-12} N$ and $G=6.67408 \times 10^{-11} m^3 kg^{-1} s^{-2}$ , what is the radius between the two masses? Round to the nearest tenth.

Hint: $\frac{\text{kg\:m}}{s^2}=1 \text{Newton}$

Possible Answers:

$r=99.80\ m$

$r=99.70\ m$

$r=99.90\ m$

$r=100\ m$

$r=99.60\ m$

Correct answer:

$r=99.80\ m$

Explanation:

The first step is to plug in all the values into the equation.

$1.34\times10^{-12} N=\frac{6.67408\times10^{-11}m^3kg^{-1}s^{-2}\cdot 10kg\cdot 20kg}{r^2}$

Now we will solve for .

$r^2=-\frac{6.67408\times10^{-11}m^3kg^{-1}s^{-2}\cdot 10kg\cdot 20kg}{1.34\times10^{-12} N}$

$r^2=\frac{1.334816\times10^{-8}m^3kg^{-1}s^{-2} kg^2}{1.34\times10^{-12} N}$

$r^2=9961.313\:m^2$

Take the square root on each side

$r=\sqrt{9961.313\:m^2}=99.80\ m$

Report an Error

Example Question #1129 : Algebra

If g(x) = 3x+2 , what is the value of g(-2) ?

Possible Answers:

Correct answer:

Explanation:

g(x) = 3x+2

g(-2) = 3(-2)+2=-6+2=-4

Report an Error

View SAT Mathematics Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Zachary
Certified Tutor

Yale University, Bachelor of Science, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Houston, SAT Courses & Classes in Miami, ISEE Courses & Classes in Denver, GRE Courses & Classes in Miami, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Miami, ISEE Courses & Classes in Houston, SAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Washington DC, ACT Courses & Classes in Philadelphia

Popular Test Prep

LSAT Test Prep in San Diego, ISEE Test Prep in Denver, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Phoenix, GMAT Test Prep in Seattle, GMAT Test Prep in Miami, ISEE Test Prep in Miami, GMAT Test Prep in New York City, ACT Test Prep in Washington DC, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Algebra

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1121 : Algebra

Example Question #1122 : Algebra

Example Question #1123 : Algebra

Example Question #1124 : Algebra

Example Question #1124 : Algebra

Example Question #1125 : Algebra

Example Question #1126 : Algebra

Example Question #1127 : Algebra

Example Question #1128 : Algebra

Example Question #1129 : Algebra

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: