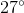We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Trigonometry

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Finding Sides With Trigonometry

The area of a regular pentagon is 1,000. Give its perimeter to the nearest whole number.

Possible Answers:

121

118

107

199

Correct answer:

121

Explanation:

A regular pentagon can be divided into ten congruent triangles by its five radii and its five apothems. Each triangle has the following shape:

Thingy_1

The area of one such triangle is $\frac{1}{2}ab$ , so the area of the entire pentagon is ten times this, or $10 \cdot \frac{1}{2}ab = 5ab$ .

The area of the pentagon is 1,000, so

5ab = 1,000

ab = 200

Also,

$\frac{a}{b} = \tan 54^{\circ }$ , or equivalently, $a=b \tan 54^{\circ }$ , so we solve for in the equation:

$b \tan 54^{ \circ } \cdot b = 200$

$b^{2} \tan 54^{ \circ } = 200$

$b^{2} = \frac{200}{\tan 54^{ \circ }} \approx \frac{200}{ 1.3764} \approx 145.3$

$b \approx \sqrt{145.3} \approx 12.1$

The perimeter is ten times this, or 121.

Report an Error

Example Question #1 : Trigonometry

The area of a regular dodecagon (twelve-sided polygon) is 600. Give its perimeter to the nearest whole number.

Possible Answers:

102

147

129

Correct answer:

Explanation:

A regular dodecagon can be divided into twenty-four congruent triangles by its twelve radii and its twelve apothems, each of which is shaped as shown:

Thingy_2

The area of one such triangle is $\frac{1}{2}ab$ , so the area of the entire dodecagon is twenty-four times this, or

$24 \cdot \frac{1}{2}ab = 12ab$ .

The area of the dodecagon is 600, so

12ab = 600 , or

ab = 50 .

Also,

$\frac{a}{b} = \tan 75^{\circ }$ , or equivalently, $a=b \tan 75^{\circ }$ , so solve for in the equation

$b \tan 75^{ \circ } \cdot b =50$

Solve for :

$b^{2} \cdot \tan 75^{ \circ } = 50$

$b^{2} = \frac{50}{ \tan 75^{ \circ }} \approx \frac{50}{ 3.7321} \approx 13.4$

$b \approx \sqrt{13.4} \approx 3.66$

The perimeter is twenty-four times this:

$P \approx 3.66 \cdot 24 \approx 88$

Report an Error

Example Question #1 : Trigonometry

The area of a regular nonagon (nine-sided polygon) is 900. Give its perimeter to the nearest whole number.

Possible Answers:

165

109

137

Correct answer:

109

Explanation:

A regular nonagon can be divided into eighteen congruent triangles by its nine radii and its nine apothems, each of which is shaped as shown:

Thingy_1

The area of one such triangle is $\frac{1}{2}ab$ , so the area of the entire nonagon is eighteen times this, or $18 \cdot \frac{1}{2}ab = 9ab$ . Since the area is 900,

9ab = 900 , or

ab= 100 .

Also,

$\frac{a}{b} = \tan 70^{\circ }$ , or equivalently, $a=b \tan 70^{\circ }$ , so solve for in the equation

$b \tan 70^{\circ } \cdot b= 100$

$b ^{2} \cdot \tan 70^{\circ } = 100$

$b ^{2} = \frac{100}{\tan 70^{\circ } } \approx \frac{100}{ 2.7475 } \approx 36.40$

$b \approx \sqrt{36.40} \approx 6.03$

The perimeter of the nonagon is eighteen times this:

$18 \cdot 6.03 \approx 109$ , the correct response.

Report an Error

Example Question #2 : Finding Sides With Trigonometry

A nonagon is a nine-sided polygon.

Nonagon ABCDEFGHI has diagonal $\overline{AC}$ with length 10. To the nearest tenth, give the length of one side.

Possible Answers:

8.7

6.2

5.3

5.9

8.3

Correct answer:

5.3

Explanation:

Construct the nonagon with diagonal $\overline{AC}$ .

We will concern ourselves with finding the length of $\overline{BC}$ .

Since $m \angle ABC = \frac{(9-2)\cdot 180^{ \circ}}{9}= 140 ^{ \circ}$ , and $\Delta ABC$ is isosceles, then

$m \angle BAC = \frac{1}{2} (180^{\circ } - 140^{\circ }) = 20^{\circ }$

The following diagram is formed (limiiting ourselves to $\Delta ABC$ ):

Decagon

By the Law of Sines,

$\frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\frac{BC}{\sin 20^{\circ }} = \frac{10} {\sin 140^{\circ }}$

$BC= \frac{10\sin 20^{\circ }} {\sin 140^{\circ }}$

$BC\approx \frac{10\cdot 0.3420} {0.6428}$

$BC \approx 5.3$

Report an Error

Example Question #1 : Trigonometry

Give the length of one side of a regular pentagon whose diagonals measure 10 each. (Nearest tenth)

Possible Answers:

5.8

8.5

7.3

5.4

6.2

Correct answer:

6.2

Explanation:

Construct the pentagon with diagonal $\overline{AC}$ .

We will concern ourselves with finding the length of $\overline{BC}$ .

Since $m \angle ABC = \frac{(5-2)\cdot 180^{ \circ}}{5}= 108 ^{ \circ}$ , and $\Delta ABC$ is isosceles, then

$m \angle BAC = \frac{1}{2} (180^{\circ } - 108^{\circ }) = 36^{\circ }$

The following diagram is formed:

Pentagon

By the Law of Sines,

$\frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\frac{BC}{\sin 36^{\circ }} = \frac{10} {\sin 108^{\circ }}$

$BC= \frac{10\sin 36^{\circ }} {\sin 108^{\circ }}$

$BC\approx \frac{10\cdot 0.5878} {0.9511}$

$BC \approx 6.2$

Report an Error

Example Question #1 : Trigonometry

In $\bigtriangleup ABC$ :

$m \angle A = 116 ^{\circ }$

$m \angle B = 20^{\circ }$

BC = 40

Evaluate to the nearest whole unit.

Possible Answers:

105

Correct answer:

Explanation:

The Law of Sines states that given two angles of a triangle with measures $\alpha, \beta$ , and their opposite sides of lengths a,b , respectively,

$\frac{\sin \alpha}{a} = \frac{\sin \beta}{b}$ ,

or, equivalently,

$\frac{b}{\sin \beta} = \frac{a}{\sin \alpha}$ .

$\overline{AC }$ , whose length is desired, and $\overline{BC}$ , whose length is given, are opposite $\angle B$ and $\angle A$ , respectively, so, in the sine formula, set b = AC , $\beta = m \angle B = 20 ^{\circ }$ , a = BC = 40 , and $\alpha = m \angle A = 116^{\circ }$ in the Law of Sines formula, then solve for :

$\frac{AC}{\sin 20^{\circ }} = \frac{40}{\sin 116^{\circ }}$

$\frac{AC}{\sin 20^{\circ }} \cdot \sin 20^{\circ } = \frac{40}{\sin 116^{\circ }} \cdot \sin 20^{\circ }$

$AC = \frac{40}{\sin 116^{\circ }} \cdot \sin 20^{\circ }$

$\approx \frac{40}{0.8988} \cdot 0.3420$

$\approx 15$

Report an Error

Example Question #4 : Finding Sides With Trigonometry

Suppose the distance from a student's eyes to the floor is 4 feet. He stares up at the top of a tree that is 20 feet away, creating a 30 degree angle of elevation. How tall is the tree?

Possible Answers:

$10\sqrt3+4$

$\frac{20\sqrt{3}+12}{3}$

$\frac{20\sqrt{3}+4}{3}$

$\frac{20\sqrt{3}+12}{3}$

Correct answer:

$\frac{20\sqrt{3}+12}{3}$

Explanation:

The height of the tree requires using trigonometry to solve. The distance of the student to the tree (20) , partial height of the tree (P) , and the distance between the student's eyes to the top of the tree will form the right triangle.

The tangent operation will be best used for this scenario, since we have the known distance of the student to the tree, and the partial height of the tree.

Set up an equation to solve for the partial height of the tree.

$tan(\theta) = \frac{\textup{Opposite side to angle}}{\textup{Adjacent side to angle}}$

$tan(30) = \frac{P}{20}$

Multiply by 20 on both sides.

$P=20tan(30) = 20(\frac{\sqrt{3}}{3}) = \frac{20\sqrt{3}}{3}$

We will need to add this with the height of the student's eyes to the ground to get the height of the tree.

$\frac{20\sqrt{3}}{3} + 4 = \frac{20\sqrt{3}}{3} + \frac{12}{3}$

The answer is: $\frac{20\sqrt{3}+12}{3}$

Report an Error

Example Question #2 : Finding Sides With Trigonometry

A decagon is a ten-sided polygon.

Decagon ABCDEFGHIJ has diagonal $\overline{AC}$ with length 10. To the nearest tenth, give the length of one side.

Possible Answers:

8.7

6.2

5.3

8.3

5.9

Correct answer:

5.3

Explanation:

Construct the decagon with diagonal $\overline{AC}$ .

We will concern ourselves with finding the length of $\overline{BC}$ .

Since $m \angle ABC = \frac{(10-2)\cdot 180^{ \circ}}{10}= 144 ^{ \circ}$ , and $\Delta ABC$ is isosceles, then

$m \angle BAC = \frac{1}{2} (180^{\circ } - 144^{\circ }) = 18^{\circ }$

The following diagram is formed (limiting ourselves to $\Delta ABC$ ):

Decagon

By the Law of Sines,

$\frac{BC}{\sin \left (m \angle BAC \right )} = \frac{AC} {\sin \left (m \angle ABC \right )}$

$\frac{BC}{\sin 18^{\circ }} = \frac{10} {\sin 144^{\circ }}$

$BC= \frac{10\sin 18^{\circ }} {\sin 144^{\circ }}$

$BC\approx \frac{10\cdot 0.3090} {0.5878}$

$BC \approx 5.3$

Report an Error

Example Question #1 : Finding Angles With Trigonometry

In $\bigtriangleup ABC$ :

AB = 23

AC = 34

BC = 25

Evaluate $m \angle A$ to the nearest degree.

Possible Answers:

$63^{\circ }$

$43^{\circ }$

$27^{\circ }$

$47^{\circ }$

$90^{\circ }$

Correct answer:

$47^{\circ }$

Explanation:

The figure referenced is below:

Triangle z

By the Law of Cosines, the relationship of the measure of an angle $\gamma$ of a triangle and the three side lengths , , and , the sidelength opposite the aforementioned angle, is as follows:

$c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

All three side lengths are known, so we are solving for $\gamma$ . Setting

c = BC = 25 , the length of the side opposite the unknown angle;

a = AB = 23 ;

b = AC = 34 ;

and $\gamma = \cos A$ ,

We get the equation

$25^{2} =23^{2} +34^{2} - 2 (23) (34)\cos A$

$625 =529+1,156- 1,564 \cos A$

$625 =1,685 - 1,564 \cos A$

Solving for $\cos A$ :

$625 - 1,685 =1,685 - 1,564 \cos A - 1,685$

$-1.060 = - 1,564 \cos A$

$\frac{-1.060 }{- 1,564}= \frac{- 1,564 \cos A}{- 1,564}$

$\cos A \approx 0.6777$

Taking the inverse cosine:

$A = \cos ^{-1} 0.6777 \approx 47 ^{\circ }$ ,

the correct response.

Report an Error

Example Question #1 : How To Find Negative Sine

If sin(x)=0.5 , what is sin(8x) if is between and $2\pi$ ?

Possible Answers:

$-\frac{\sqrt{3}}{2}$

-0.5

-1.5

0.5

$\frac{\sqrt{3}}{2}$

Correct answer:

$-\frac{\sqrt{3}}{2}$

Explanation:

Recall that $sin(\frac{\pi}{6}) =0.5$ .

Therefore, we are looking for $sin(8*\frac{\pi}{6})$ or $sin(\frac{4\pi}{3})$ .

Now, this has a reference angle of $\frac{\pi}{3}$ , but it is in the third quadrant. This means that the value will be negative. The value of $sin(\frac{\pi}{3})$ is $\frac{\sqrt{3}}{2}$ . However, given the quadrant of our angle, it will be $-\frac{\sqrt{3}}{2}$ .

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Shakeel
Certified Tutor

View SAT Subject Test in Mathematics Level 2 Tutors

Evgenii
Certified Tutor

View SAT Subject Test in Mathematics Level 2 Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Phoenix, English Tutors in San Francisco-Bay Area, MCAT Tutors in San Francisco-Bay Area, Calculus Tutors in San Diego, Calculus Tutors in Denver, ACT Tutors in Denver, LSAT Tutors in Seattle, SAT Tutors in Miami, Calculus Tutors in Houston, Reading Tutors in Houston

Popular Courses & Classes

SSAT Courses & Classes in Seattle, SSAT Courses & Classes in Denver, Spanish Courses & Classes in New York City, ISEE Courses & Classes in Phoenix, ACT Courses & Classes in Seattle, Spanish Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Houston, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in San Diego

Popular Test Prep

ISEE Test Prep in Atlanta, GRE Test Prep in San Diego, SSAT Test Prep in Washington DC, ISEE Test Prep in Los Angeles, MCAT Test Prep in New York City, ISEE Test Prep in Washington DC, SAT Test Prep in Washington DC, SSAT Test Prep in Chicago, LSAT Test Prep in Philadelphia, ACT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Trigonometry

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Finding Sides With Trigonometry

Example Question #1 : Trigonometry

Example Question #1 : Trigonometry

Example Question #2 : Finding Sides With Trigonometry

Example Question #1 : Trigonometry

Example Question #1 : Trigonometry

Example Question #4 : Finding Sides With Trigonometry

Example Question #2 : Finding Sides With Trigonometry

Example Question #1 : Finding Angles With Trigonometry

Example Question #1 : How To Find Negative Sine

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: