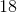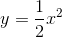We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : SAT Subject Test in Math II

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : 3 Dimensional Axes And Coordinates

Which of the following numbers comes closest to the length of line segment in three-dimensional coordinate space whose endpoints are the origin and the point (3,4,5) ?

Possible Answers:

8.5

7.5

6.5

Correct answer:

Explanation:

Use the three-dimensional version of the distance formula:

$d= \sqrt{(x_{1}-x_{2})^{2} +(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}$

$d= \sqrt{(3-0)^{2} +(4-0)^{2}+(5-0)^{2}}$

$d= \sqrt{3^{2} +4^{2}+5^{2}}$

$d= \sqrt{9+16+25}$

$d= \sqrt{50}$

$d \approx 7.1$

The closest of the five choices is 7.

Report an Error

Example Question #2 : 3 Dimensional Axes And Coordinates

A line segment $\overline{AB}$ in three-dimensional space has midpoint ; $\overline{AM}$ has midpoint .

has Cartesian coordinates $\left ( 100, \frac{1}{2}, 100\right )$ ; has Cartesian coordinates $\left ( 150, - \frac{1}{3}, -100\right )$ . Give the -coordinate of .

Possible Answers:

$-\frac{5}{6}$

$-1\frac{5}{6}$

$- 2\frac{5}{6}$

$2\frac{1}{6}$

Correct answer:

$- 2\frac{5}{6}$

Explanation:

The midpoint formula for the -coordinate

$\frac{y_{1}+y_{2}}{2}=y_{M}$

will be applied twice, once to find the -coordinate of , then again to find that of .

First, set $y_{2}=\frac{ 1 }{2}$ , the -coordinate of , and $y_{M}= - \frac{1}{3}$ , the -coordinate of , and solve for $y_{1}$ , the -coordinate of :

$\frac{y_{1}+\frac{ 1 }{2}}{2}=- \frac{1}{3}$

$y_{1}+\frac{ 1 }{2}=- \frac{2}{3}$

$y_{1} =- 1\frac{1}{6}$

Now, set $y_{2}=\frac{ 1 }{2}$ , the -coordinate of , and $y_{M}=- 1\frac{1}{6}$ , the -coordinate of , and solve for $y_{1}$ , the -coordinate of :

$\frac{y_{1}+\frac{ 1 }{2}}{2}= - 1\frac{1}{6}$

$y_{1}+\frac{ 1 }{2} = - 2\frac{1}{3}$

$y_{1} = - 2\frac{5}{6}$

Report an Error

Example Question #3 : 3 Dimensional Axes And Coordinates

A line segment in three-dimensional space has endpoints with Cartesian coordinates (-4, 1, 8) and $\left (5, -2, 7 \right )$ . To the nearest tenth, give the length of the segment.

Possible Answers:

15.1

9.5

3.0

9.1

1.7

Correct answer:

9.5

Explanation:

Use the three-dimensional version of the distance formula:

$d= \sqrt{(x_{1}-x_{2})^{2} +(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}$

$d= \sqrt{(-4-5)^{2} +(1-(-2))^{2}+(8-7)^{2}}$

$d= \sqrt{(-9)^{2} +3^{2}+1^{2}}$

$d= \sqrt{81+9+1}$

$d= \sqrt{91}$

$d \approx 9.5$

Report an Error

Example Question #4 : 3 Dimensional Axes And Coordinates

A pyramid is positioned in three-dimensional space so that its four vertices are located at the points with coordinates (6,0,0) ,(0,9,0), (0,0,12) , and the origin. Give the volume of this pyramid.

Possible Answers:

108

648

162

Correct answer:

108

Explanation:

The three segments that connect the origin to the other points are all contained in one of the -, -, and - axes. Thus, this figure can be seen as a pyramid with, as its base, a right triangle in the -plane with vertices (6,0,0) ,(0,9,0) , and the origin, and, as its altitude, the segment with the origin and (0,0, 12) as its endpoints.

The segment connecting the origin and (6,0,0) is one leg of the base and has length 6; the segment connecting the origin and (0,9,0) is the other leg of the base and has length 9; the area of the base is therefore

$B = \frac{1}{2} \cdot 6 \cdot 9 = 27$

The segment connecting the origin and (0,0, 12) is the altitude; its length - the height of the pyramid - is 12.

The volume of the pyramid is

$V = \frac{1}{3} Bh = \frac{1}{3} \cdot 27 \cdot 12 = 108$

Report an Error

Example Question #3 : 3 Dimensional Axes And Coordinates

A pyramid is positioned in three-dimensional space so that its four vertices are located at the points with coordinates (X,0,0) ,(0,Y,0), (0,0,Z) , and the origin. Give the volume of this pyramid.

Possible Answers:

$\frac{2}{3}XYZ$

$\frac{1}{2}XYZ$

$\frac{1}{3}XYZ$

$\frac{1}{6}XYZ$

XYZ

Correct answer:

$\frac{1}{6}XYZ$

Explanation:

The three segments that connect the origin to the other points are all contained in one of the -, -, and - axes. Thus, this figure can be seen as a pyramid with, as its base, a right triangle in the -plane with vertices (X,0,0) ,(0,Y,0) , and the origin, and, as its altitude, the segment with the origin and (0,0, Z) as its endpoints.

The segment connecting the origin and (X,0,0) is one leg of the base and has length ; the segment connecting the origin and (0,Y,0) is the other leg of the base and has length ; the area of the base is therefore

$B = \frac{1}{2} XY$

The segment connecting the origin and (0,0, Z) is the altitude; its length - the height of the pyramid - is .

The volume of the pyramid is

$V = \frac{1}{3} Bh = \frac{1}{3} \cdot \frac{1}{2}XY \cdot Z= \frac{1}{6}XYZ$

Report an Error

Example Question #1 : 3 Dimensional Axes And Coordinates

A line segment $\overline{AB}$ in three-dimensional space has midpoint ; $\overline{AM}$ has midpoint .

has Cartesian coordinates $\left ( 100, \frac{1}{2}, 100\right )$ ; has Cartesian coordinates $\left ( 150, - \frac{1}{3}, -100\right )$ . Give the -coordinate of .

Possible Answers:

Correct answer:

Explanation:

The midpoint formula for the -coordinate

$\frac{z_{1}+z_{2}}{2}=z_{M}$

will be applied twice, once to find the -coordinate of , then again to find that of .

First, set $z_{2}= 100$ , the -coordinate of , and $z_{M}= -100$ , the -coordinate of , and solve for $z_{1}$ , the -coordinate of :

$\frac{z_{1}+100}{2}=-100$

$z_{1}+100 = -200$

$z_{1}=-300$

Now, set $z_{2}= 100$ , the -coordinate of , and $z_{M}= -300$ , the -coordinate of , and solve for $z_{1}$ , the -coordinate of :

$\frac{z_{1}+100}{2}= -300$

$z_{1}+100 = -600$

$z_{1}=-700$

Report an Error

Example Question #3 : 3 Dimensional Axes And Coordinates

A line segment $\overline{AB}$ in three-dimensional space has midpoint ; $\overline{AM}$ has midpoint .

has Cartesian coordinates $\left ( 100, \frac{1}{2}, 100\right )$ ; has Cartesian coordinates $\left ( 150, - \frac{1}{3}, -100\right )$ . Give the -coordinate of .

Possible Answers:

500

300

250

Correct answer:

300

Explanation:

The midpoint formula for the -coordinate

$\frac{x_{1}+x_{2}}{2}= x_{M}$

will be applied twice, once to find the -coordinate of , then again to find that of .

First, set $x_{2}= 100$ , the -coordinate of , and $x_{M}= 150$ , the -coordinate of , and solve for $x_{1}$ , the -coordinate of :

$\frac{x_{1}+100}{2}= 150$

$x_{1}+100 = 300$

$x_{1}=200$

Now, set $x_{2}= 100$ , the -coordinate of , and $x_{M}= 200$ , the -coordinate of , and solve for $x_{1}$ , the -coordinate of :

$\frac{x_{1}+100}{2}= 200$

$x_{1}+100 = 400$

$x_{1}=300$

Report an Error

Example Question #1 : Other 3 Dimensional Geometry

A convex polyhedron has twenty faces and thirty-six vertices. How many edges does it have?

Possible Answers:

Correct answer:

Explanation:

The number of vertices , edges , and faces of any convex polyhedron are related by By Euler's Formula:

V- E + F = 2

Setting V= 36, F = 20 and solving for :

36- E + 20 = 2

56- E = 2

E = 54

The polyhedron has 54 edges.

Report an Error

Example Question #1 : Coordinate Geometry

Which of the following equations represent a parabola?

Possible Answers:

$y=\frac{1}{2x^2}$

$y=\frac{1}{2}x^2$

$y=\frac{1}{2x}$

y=2^x

y^2 = x^2

Correct answer:

$y=\frac{1}{2}x^2$

Explanation:

The parabola is represented in the form y=ax^2+bx+c . If there is a variable in the denominator or as an exponent, it is not a parabola.

The only equation that has an order of two is: $y=\frac{1}{2}x^2$

Report an Error

Example Question #2 : Coordinate Geometry

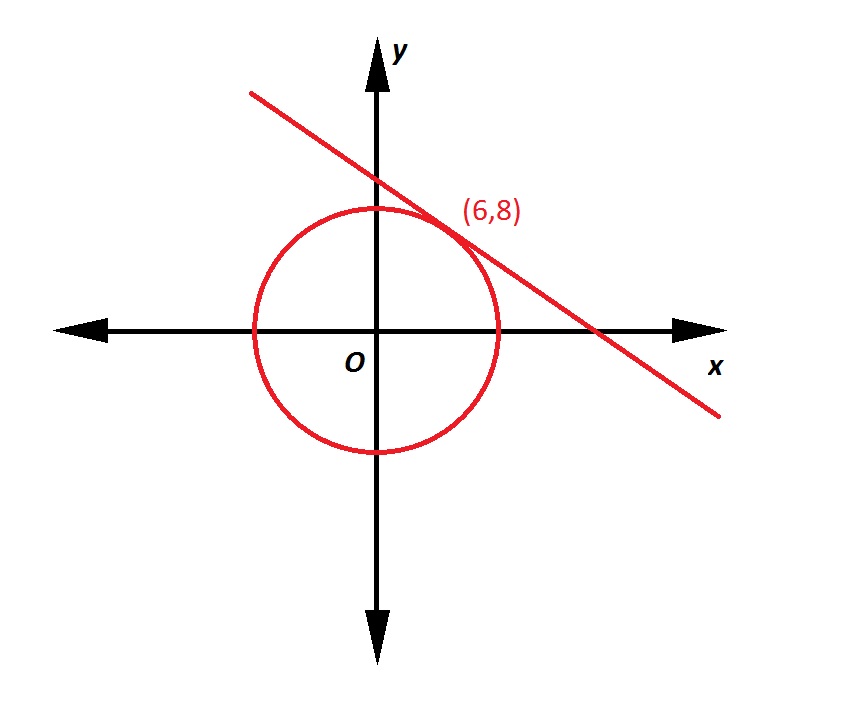
Circle

Refer to the above figure. The circle has its center at the origin. What is the equation of the circle?

Possible Answers:

$\frac{x^{2}}{36}- \frac{y^{2} }{64}= 1$

$x^{2}+ y^{2} = 100$

$\frac{x^{2}}{36}+ \frac{y^{2} }{64}= 1$

$\frac{y^{2} }{64 } - \frac{x^{2}}{36} = 1$

$x^{2}+ y^{2} = 1 0$

Correct answer:

$x^{2}+ y^{2} = 100$

Explanation:

The equation of a circle with center (h, k) and radius is

$(x-h)^{2}+ \left ( y - k\right )^{2} = r^{2}$

The center is at the origin, or (0,0) , so h = k = 0 . To find $r^{2}$ , use the distance formula as follows:

$r^{2} = \left ( 6-0\right )^{2} +\left ( 8 -0 \right )^{2} = 6^{2}+8^{2} = 36 + 64 = 100$

Note that we do not actually need to find .

We can now write the equation of the circle:

$(x-0)^{2}+ \left ( y - 0\right )^{2} = 100$

$x^{2}+y^{2} = 100$

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

View SAT Subject Test in Mathematics Level 2 Tutors

Rodolfo
Certified Tutor

The University of Texas at San Antonio, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 2 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Miami, ACT Tutors in Houston, SAT Tutors in Seattle, Spanish Tutors in Miami, French Tutors in Seattle, ACT Tutors in Dallas Fort Worth, Chemistry Tutors in Phoenix, Calculus Tutors in Atlanta, Calculus Tutors in Washington DC, SAT Tutors in Los Angeles

Popular Courses & Classes

Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Atlanta, ACT Courses & Classes in San Diego, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, SAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in San Diego, SAT Test Prep in Washington DC, GRE Test Prep in Philadelphia, ACT Test Prep in Phoenix, GMAT Test Prep in Phoenix, SAT Test Prep in Phoenix, ACT Test Prep in Atlanta, ACT Test Prep in Boston, SSAT Test Prep in Miami, SAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : SAT Subject Test in Math II

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : 3 Dimensional Axes And Coordinates

Example Question #2 : 3 Dimensional Axes And Coordinates

Example Question #3 : 3 Dimensional Axes And Coordinates

Example Question #4 : 3 Dimensional Axes And Coordinates

Example Question #3 : 3 Dimensional Axes And Coordinates

Example Question #1 : 3 Dimensional Axes And Coordinates

Example Question #3 : 3 Dimensional Axes And Coordinates

Example Question #1 : Other 3 Dimensional Geometry

Example Question #1 : Coordinate Geometry

Example Question #2 : Coordinate Geometry

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: